Generative AI for automating appeals

Focusing on architecture, May 2024

Motivation, via a comparison to the show 'Grand Designs'

One of my favorite light-hearted TV shows of late is the British home design marvel 'Grand Designs' (as I am writing this, it is free to stream on YouTube). The show - hosted by British designed Kevin McCloud - follows amateur, first-time builders as they set out to construct their own home. Almost without fail, the new builders go from being very excited about everything the new home will bring them, to miserable and downtrodden as delays and surprise costs push them to a breaking point. However, the episode (almost) always ends with a beautiful building, a beaming builder, and an uplifting narrative from the host about how this particular modern glass box represents a great triumph of the human spirit. And I tend to agree with him. Building your first home takes an admirable amount of bravery and perseverance. Additionally, the disparate backgrounds of the people on show sometimes result in truly unique and beautiful buildings.

When watching the show, I often see parallels between the trials and tribulations faced by the home-owner-turned-project-managers and those faced when managing tech projects. I am not the first to draw such parallels - several participants on the show, as well as the authors of the project management book 'How Big Things Get Done' Bent Flyvbjerg and Dan Gardener, have noted the similarities between large projects in different mediums.

Flyvbjerg and Gardener takes this observation further by collecting and collating data from thousands of big projects across different sectors. Like the participants in 'Grand Designs', these projects also usually go over budget and over time despite being run by professionals. However, there a few common features of successful projects that the authors discuss. The feature most relevant to this post, is that successful (here, meaning on-time and on-budget) big projects are often made up of smaller repeated modules. One of the most memorable examples of the project management principle is the Empire State Building - an architectural marvel that was also a project management success. Each floor of the building is very similar. This similarity allowed worker to rapidly increase their speed at they built more floors, because they could learn from the mistakes they made on lower floors. As an individual contributor trying to build a new data science team in an established company, I am often thinking about how single projects can be used as smaller, repeatable building blocks to bring the team towards a grander vision.

One of these instances occurred while participating in meetings regarding how to best incorporate new generative AI technologies into our business practices. Here, it was important to balance good project management with minimizing risk to patients and maximizing benefit to the company when considering use cases. And there are no shortages of resources listing all the possible use cases of generative AI in healthcare. The problem is picking the best one to start with. If I were considering only project management, I would pick a simple app that used one foundation model, and one method for reducing hallucinations. This set up is common to many generative AI apps, and lessons learned in the simple case could be brought to other use cases. If I were only considering the minimal cost patients, I would probably start with some system that would be used only internally. Bain did the hard work of considering the maximizing business value part of the cost function and identified a few cases that stood out above the rest. 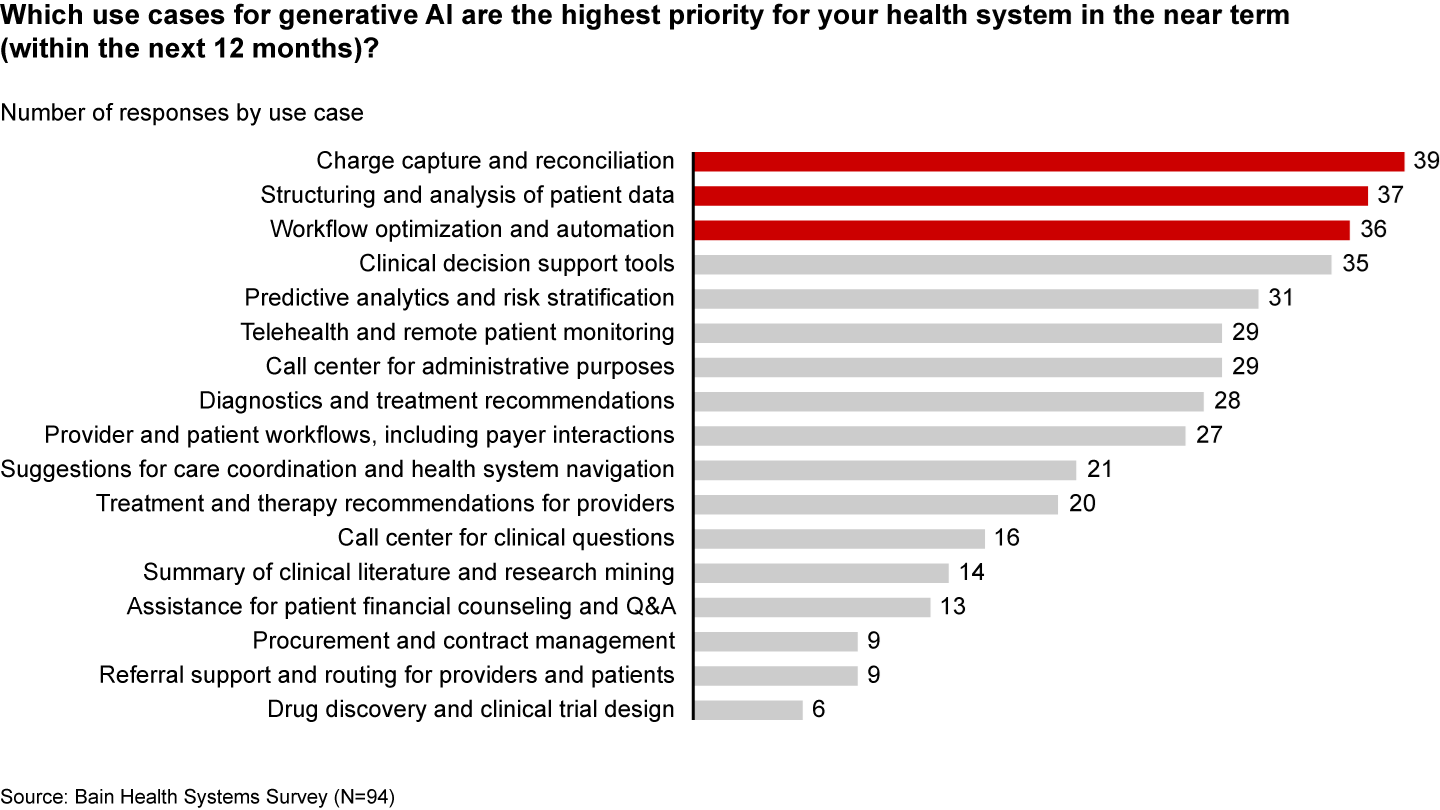One of these use cases includes automating appeals. Part of their reasoning comes from knowledge that payors automate denials with the assumption that appeals are exceedingly rare. This means that denial are issued liberally and many appeals are likely to provide adjustments. Additionally, automatic letter writing is not something that can easily be achieved with simpler methodologies. The appeals use case does pretty well with other parts of the cost function too. Automating appeals can have big impacts on revenue, but zero to low impact on patient care if something goes wrong. Lastly, the architecture for an automated letter drafting system is like many other kinds of generative AI use cases. Therefore, choosing this as one of the first use cases can set you up well to scale in the future.

Generative AI Background

While an out-of-the-box LLM could probably generate a readable letter, it would likely hallucinate details about the patient or produce an overly generic letter if no modifications were made. We need to find a way to reduce these hallucinations and give the LLM access to specific information. This is why, at a high level, a generative AI system for automating appeals would have two main components: (1) a large language model (LLM) and (2) a method for retrieving documents relevant to the denial. Step 2 - the retrieval system - helps to address both the hallucinations and the lack of specific information. More specifically, step 2 refers to retrieval augmented generation (RAG). A process by which extra context is added to the prompt given to LLM to help it perform on specific tasks. From a data science perspective, setting up the retrieval system is a primary source of complexity in these apps.

Another way to reduce hallucinations is to fine tune the foundation LLM model on data relevant to denial letters. Since both the RAG system and fine-tuning can help reduce hallucinations, we'll go more in depth into the differences between the two next.

RAG vs Fine-tuning

RAG: RAG (or retrieval augmented generation) is a process by which relevant context is added to the query to an LLM in hopes of getting more accurate and traceable answers. Retrieving context often relies on converting both the original query and the bank of contexts to vectors, matching the query-vector to the various context-vectors, and appending the contexts that are the most like the query. Performance of this retriever should generally be evaluated and periodically monitored. The documents available, the retrieval algorithm, and the vector embedding model are common thing to tweak during the process of building a RAG app.

One of the benefits of RAG is that it is computationally fairly cheap and easy to update compared to fine-tuning. Additionally, if the relevant contexts change, all you have to do update your system is replace the documents, rather than retune the whole model. This is especially important in healthcare contexts where medical policies and contracts are changing on a yearly basis.

Fine-tuning: In general, fine-tuning refers to the process of taking a pretrained model and retraining it on a task different from its original purpose. When people talk about fine-tuning in generative AI applications, they are usually talking about taking an existing foundation model and training it to perform well in more specialized setting while retaining its general language capabilities, but you could also fine-tune the embedding models used in the RAG system (more on this later).

Fine-tuning has many of the same problems training other deep neural network models has. It can be computational very expensive to fine tune a model for a production application (even small LLMs have 10s of billions of parameters). While there are methods to minimize these costs (like parameter efficient fine-tuning, PEFT), they can still be prohibitive in some cases. Additionally, since fine-tuning will change the weights of the foundation model, it is wise to evaluate your final model both on its performance on the new task you are fine-tuning it on, and its general language accuracy too.

To summarize:

• Both RAG systems and fine-tuning can reduce hallucinations, but only RAG systems can provide the LLM with case specific documents.
• Both RAG systems and fine-tuning require high quality, context specific data.
• Fine-tuning requires more compute resources. These resources are spent on the tuning itself, and in the time it takes to re-evaluate the model after tuning.
• It is easier to update the corpus of documents for the RAG system when policies change than to retune an LLM.

A state-of-the art approach would include both RAG and fine-tuning, though it would be possible to build a performant app that only used the RAG system. The logic behind this distinction is that the model might benefit from learning the nuances of medical billing communication and jargon through fine-tuning, but it needs to be able to pull documents specific to the patient to draft an acceptable letter. For a first use case generative AI app targeted at automating denials, I would recommend starting with just a RAG system. After the RAG system is working, fine-tuning could be added if necessary to improve performance. However, since including both often increases performance, discussions of the specific structure of this system will incorporate fine-tuning the foundation model as well.

Example Architecture

Here, we show an example architecture for implementing a generative AI system for automating appeals.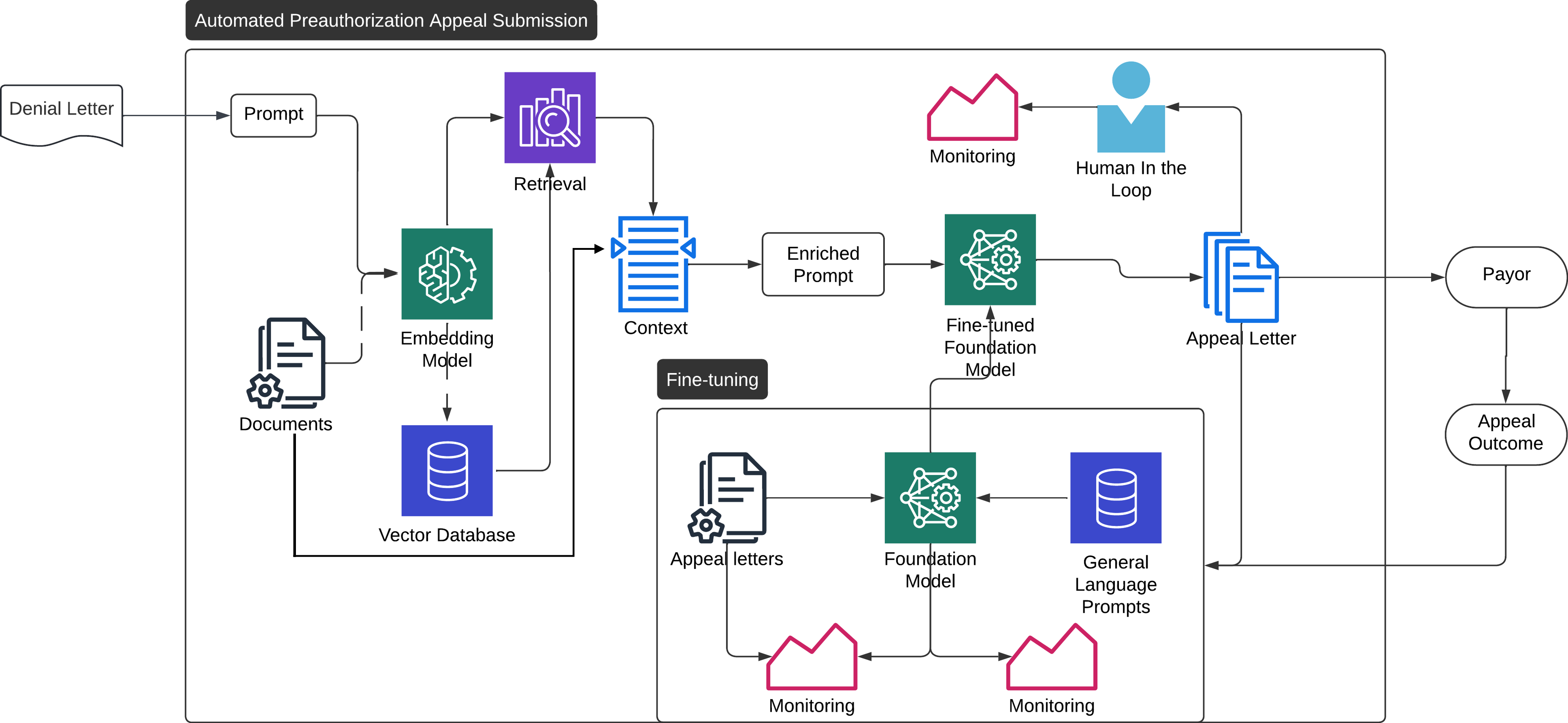 The high-level flow of information through the system is:

1. Denial letter comes in, is parsed to text, and embedded as a vector.
2. Relevant information that can pulled directly from metadata are pulled.
3. The denial letter embedding is compared to the information in the vector database. The best matches are pulled.
4. The three pieces of information from the previous steps are combined into a query for the LLM
5. The new query + context is sent to the LLM (fine-tuned or otherwise), which generates an appeal letter.
6. The letter is stored for later evaluation.
7. The letter is either reviewed by a specialist or sent directly to the payor.
8. The payors response is recorded and monitored to assure the consistent performance of the system.

There are a few main components that need setting up before the system can started generating appeals:

Vector database

The RAG system will need access to all the relevant information it would need to write the appeal letter. Some of this information can likely be passed directly to the app based on metadata about the denial, and some of it will need to be searched for. For example, medical notes unique to a specific patient could be pulled based on patient identifiers, while grabbing the specific part of the medical policy relevant to the procedure might require a search. The exact division will likely depend on the data ecosystem at a given institution. Any information that needs to be searched for will need to be parsed into chunks of text, encoded as a vector, and stored in a vector database. Most databases will be structured as some kind of hierarchical small world network, but sometimes more specialized topologies can be appropriate for some types of data. For example, this paper explored using a tree structure for internal company data, which is hierarchical.

Embedding model

The embedding model is responsible for transforming the documents and queries to vector representations. Depending on the data the model is trained on, the model will likely have slightly different distances between similar words. Since healthcare is a pretty niche topic, I’d recommend starting with some kind of clinical embedding mode such as ClinBERT. This model is trained on clinical notes, if you are working with a vendor who provides embedding models specific to medical claims that would likely provide even better performance. You can also fine-tune embedding models on in house data to create more useful embeddings.

Retrieval

How to quickly retrieve the ‘best’ context is remains an area of active research. The simplest and most common method uses a KNN or a similar algorithm to pull the ‘top-k’ nearest neighbors. FAISS or ANNOY are common tools for generating and searching embedding spaces. Using ElasticSearch together with FAISS or ANNOY can combine these vector searches with standard text or metadata-based searches. Ideally, you would also set up some kind of evaluation of the quality of the retrieved documents. A common way to evaluate these systems is to have raters look through results and mark the success of the retrieval based on a defined rubric.

Foundation model and fine-tuning

Some consideration must be given to the foundation LLM at the start. In healthcare use cases, it is especially important to use foundation models that are HIPPA compliant and will not reuse queries in training sets, even if the data have already been deidentified. Additionally, fine-tuning requires setting up some kind of new task to train the model on more specific contexts. For this application, predicting the success of appeals from letters would be a good task, though it requires a large volume of appeal letters. In addition to the standard monitoring and evaluation required to fine-tune the foundation model, you will also want to set up some method of evaluating the general language capabilities of the fin- tuned model. There are several databases and packages of question-answer style prompts available for these purposes. While you're at it, you might as well throw in some extra monitoring for bias as well.

Other parameters: In addition to privacy, there are other features of the foundation model to consider when selecting which one to start with:

• Number of parameters: This parameter is especially important if fine-tuning is going to be an integral part of your strategy. More parameters generally mean higher costs to tuning, though larger models might also often afford better performance.
• Maximum context size: Different foundation models have different limits for the largest prompt they will accept. Lower limits mean that you cannot include as much context in your query. While it might seem intuitive that more context would lead to better performance, that is not always the case. Regardless of your foundation model choice the amount of context to include is a parameter you can have to tune to improve performance.
• Transparency: Different foundation models adhere to different levels of transparency. More transparent models allow you to have more confidence in the model’s performance and blind spots. Additionally, if the model demonstrates bias in specific situations more information about the model can often lead to faster fixes. In healthcare, minimizing bias in anything impacting patient care (or payments, in this case) should be considered.

Conclusion

I've tried to provide the motivation, and the roadmap for an automated appeals system as a first step towards building robust generative AI for healthcare. This use case could bring in lots of uncaptured revenue for a company without risking patient care. Automating appeals can also help healthcare companies keep pace with payors. All while creating a nice template for future RAG applications. Now that we have laid out the vision and the plan, this would be the part of the 'Grand Designs' episode where the host foreshadows the setbacks to come and gives a knowing smile to the audience. While I do not currently have the benefit of hindsight, it is worth pointing out any generative AI app in healthcare with be difficult. The US healthcare system is extremely complicated, and any RAG system faces an uphill battle trying to parse between the subtle differences in contract language for the multitude of different payors, contracts, medical policies, etc. But I think it's worth the struggle. With an eye towards simplicity, modularity, and good project management, these apps can be technical and management successes.

Other Resources

• Intro to LLMs series
• Original RAG paper
• Jerry Liu's talk on RAG systems and methods for improvement

A non-linear, inefficient example of an 'academia-to-industry' career path

More specifically, a computational neuroscience to enterprise data science path, Feb 2023

When I started my PhD, I already suspected that I did not want to become a professor. However, I was very anxious about the limited knowledge I had regarding non-academic career opportunities in my field. Due to this anxiety, I attended every career panel, read every Twitter thread, and consumed every unsolicited piece of advice about post-PhD non-academic jobs as if they were gospel. These resources were useful, especially early in the process, and I am grateful to everyone who offered their advice. However, my job search still felt consistently surprising and out of my control.

My intention here is not to present a prescriptive approach to job searches but to add one example of the diverse range of non-linear paths that exist. My hope is that this account will offer some helpful tips for those looking for guidance or solidarity for those who feel confused about the process.

In this account, I will try to walk through the steps I took during the job search and share my observations and surprises along the way. As I am not an experienced writer, I will also include photographs of my cat Noodles to better convey my emotions during the process.

My background

It's important to acknowledge that I had a lot working in my favor to bring me to the PhD and industry science. For one, my dad worked in BioTech with a PhD, which made higher education and related fields an easy choice for me. Moreover, throughout the process I did not have to factor in any extra financial or caretaking responsibilities when making decisions.

What I sought from a career path was job security, the ability to work in different locations, an environment that wasn't cutthroat, external validation of my work, good pay, fast-paced projects with clear endpoints (that were not papers), opportunities for creative problem-solving, the utilization of my existing skills, and a sense that my work was not inherently detrimental to the world. After considering my priorities, I concluded that a job in some kind of scienc-y industry (probably data science), outside of academia, could meet most of my criteria.

My timeline

I began my job search in earnest by interning at a university-affiliated research center (UARC) in June 2020. While I learned valuable skills during this internship, I ultimately decided to pursue a job that aligned better with my priorities. That being said, I believe UARCs are an excellent option for academics who enjoy their work but desire a more stable, higher-paying environment.

In January 2021, after defending my PhD I chose to put off applying for jobs during the pandemic's peak by creating a more senior position in my current PhD lab. I also believed that I still had skills to develop before becoming a competitive candidate on the market, although this wasn't really true. I designed a data scientist position for my PhD lab that would let me do work as close as possible to the job I wanted, while still being part of academia.

I stayed in this academic data scientist position for 6 months, and then did my first non-academic job search in the summer of 2021 (upon reflection, this was also a very tumultuous time to be looking for tech jobs). I sent about 40 applications, got 5 interviews, and 1 offer at a Children's Hospital. This position was another academic data scientist position - not really the end point I had envisioned. I accepted the position, partially because I was feeling exhausted by the search process, but mostly because I anticipated that a new environment would provide additional learning opportunities.

After working at the Children's Hospital for about 6 months (now summer of 2022), I decided to start applying for jobs again. I applied to 10 positions, got called in for 1 interview, and received 1 offer. This time, the position was decidedly outside of academia, and seemed to meet most of the criteria I had. All in all, it took me 2 years, 50 applications, 6 interviews, and 2 offers to get my first non-academic job. Based on my conversations with other individuals who have transitioned from academia to industry, these numbers seem to be typical. The rest of the post is dedicated to giving more context to each of the steps I took to get there.

Understanding what you want

Even if you know that you don't want to stay in academia, understanding what you do want is a crucial first step. It may seem obvious, but deeply examining what you value in life, why you value it, and how your career fits into those values can be challenging. It may even force you to confront uncomfortable truths about yourself and reconcile conflicting desires. Online question prompts can help you get started, but most of my process involved conversations with friends and my partner.

After I spent a lot of time confronting my own demons, the task of wading through a quagmire of job ads and career paths without an experienced mentor to guide me felt daunting. Part of me hoped that once I committed to a career path and made myself vulnerable enough to tell people my decision, a job would just materialize as an email in my inbox one day. But - unsurprisingly - that didn't happen, and the job search process continued to be challenging. However, the clarity I had about my values, paired with acceptance that they might change really helped me streamline my search and weather the process.

Understanding what's out there

After getting some sense of what I wanted, it was time to see how different job titles and work sectors mapped onto those criteria. During the early stages of my PhD, I used to believe that the term 'industry' meant 'anything not academic'. I also held the misconception that the only distinguishing factor between the two sectors was that industry jobs were faster-paced and paid better. However, I have come to realize that this is not the case, and individuals outside of academia may find it perplexing if you describe their work as 'industry' when they actually work for a non-profit organization. Through the resources I have gathered since, I have created a more precise graphical representation of the job sectors. Characteristic of a data science, it is designed to resemble some kind of dimensionality reduction output. Here, the two most important dimensions are intellectual freedom, and project duration. Uncharacteristic of a data science, the plot involves no data, only vibes and assorted perspectives I've collected over time.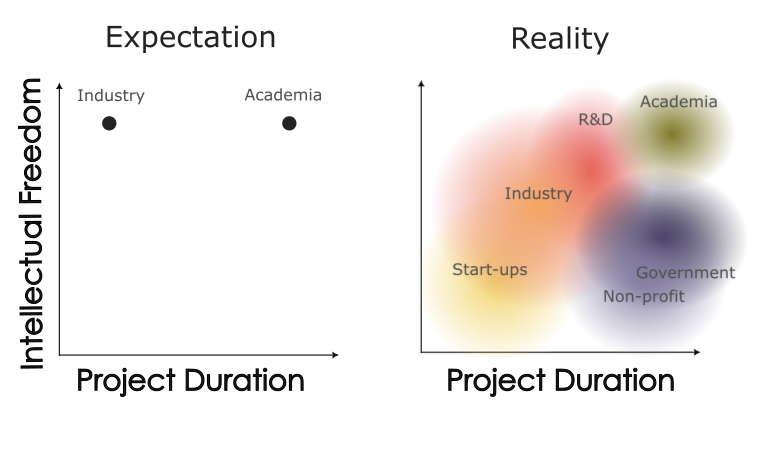

The first graphic describes my early impressions of industry early in my PhD. I formed my ideas based on interactions with industry scientists who focused on a narrow type of R&D research. These scientists typically worked for well-funded R&D divisions and believed they had as much intellectual freedom as they would have had in academia. The second graphic reflects my current understanding, which has evolved. Notably, each sector is represented by a density rather than a point estimate (the text placement was chosen for visualization purposes and does not reflect the density centroid). As a result, there is considerable overlap between categories. While some industry, government, or non-profit positions offer as much intellectual freedom as academia, many do not. The same is true for pace.

In each of these sectors, there are various job titles related to 'data science'. While the majority of postings will list 'data scientist' as the job title, most could be described as a more granular level by one of several categories. The book 'Build a Career in Data Science' uses a graphical representation to illustrate these different jobs based on their skillsets. I have recreated this graphic below. The three corners represent three common types of skills valued in data science: math/stats (+/-), coding/databases (<>), and domain knowledge/communication (the stack of books). Different jobs emphasize different combinations of these skills. For instance, the 'decision scientist' data scientist depends mostly on communication or domain expertise and math/stats skills, while the 'data analyst' data scientist relies more on databases and domain expertise, and the 'MLOps' data scientist relies heavily on coding/databases and math/stats. Additionally, there are some data science-adjacent positions that heavily rely on one of these types of skills (i.e., research scientist or data engineer). The purpose of this post is not to provide a detailed description of each of these jobs, but to give a starting point to dive in further. The book from which this graphic was taken is an excellent resource to learn more. 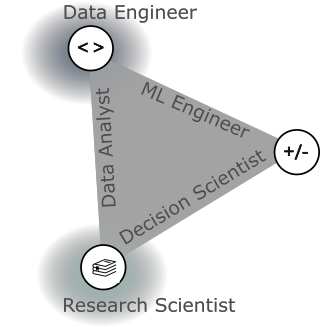When I began my search for data science jobs, I was overwhelmed by the variety of skill sets listed in different job ads. This led me to the false assumption that I needed to be an expert in all these skills to be a competitive candidate for any data science job. However, the key takeaway from the graphic is that you do not need to excel in all the skills to get a job in data science. Instead, you can leverage your existing strengths to find a data scientist role that is a good match for you.

It's worth noting that data science is a popular title right now, and some companies may use it to refer to a wide range of positions to attract top talent. Being selective with the job ads you apply to based on the listed skills can help cut through some of this noise. Furthermore, if a job ad requires expertise in all aspects of data work, it could be a red flag indicating that the company does not fully understand the diverse range of roles required to effectively use data.

Understanding skillsets for data science

I eventually decided to pursue a career as a decision scientist/data scientist. As shown in the previous graphic, this role places more emphasis on math and domain knowledge rather than coding/database skills, but companies often have specific skill requirements for these positions.

To better understand the necessary skills for this role, I have compiled a list of skills that I believe are common across different data science job postings. I categorized them into three groups: skills that I acquired during my PhD without consciously trying to develop them, skills that I intentionally worked on during my PhD, and skills that I think would be difficult or impossible to gain solely through a PhD program.

Things I had gained by getting my PhD without really trying

• project management
• breaking down complex problems into actionable steps
• statistics
• experimentation and hypothesis testing
• biomedical domain expertise
• coding in Python or R (I realize that this is not a given for everyone)
• the ability to learn new technical skills and methods
• the ability to select between different methods
• coming up with new projects and next steps

Things I explicitly tried to work into my PhD, even though they weren't required

• coding in SQL
• some advanced machine learning and statistics (note that this says some, not all)
• exposure to JavaScript and web apps (most jobs don't expect you to know JavaScript, but it was useful to understand how a web app worked)
• some best practices in coding: github, packaging python code, unittesting and reproducible machine learning pipelines (like MLFlow)

Things that I could not figure out how to gain through my PhD

• Specific database management tools that cost money Universities aren't willing to pay for (Snowflake, AWS, etc.)
• How to prioritize projects based on business value*
• Knowledge of different business models (healthcare is wild)*
• Knowledge of how to design projects that provide value to someone outside of a University (i.e. marketing, accounting, etc.)*

* I often dismissed these points during my job search because I was confident I would be able to gain these skills on the job, but they are extremely important. I'll elaborate on this a bit more in the next section.

Understanding industry's perception of academics

At this point, I knew both what jobs I was interested in and roughly which ones I had the skills to do. However, me deciding I had those skills and me convincing other people I had them were two different things. I had to learn a lot about how people in other sectors perceived academics to be successful on the market.

During my PhD program, most of the information I received about industry jobs was presented at events sponsored by the program. These events had a generally positive outlook on job prospects after graduation and emphasized that PhD candidates had many desirable skills, and would have many options after graduating. While this was not inaccurate, it gave me the impression that most companies explicitly sought out PhD graduates and understood what a PhD entailed. This impression was not entirely true in practice. While some companies, particularly R&D departments, have a history of hiring academics and are more familiar with interpreting academic accomplishments, this is less common in the business/enterprise data science field.

While most people in industry recognized that PhDs foster independent work and decision-making. I found that I had to work harder to convince companies of my technical skills, project management abilities, and communication skills. Additionally, industry employers expected PhD graduates to have no business knowledge, to have trouble prioritizing the interests of the company over their own professional development, and to have trouble working with teams at a fast pace. These were significant challenges I had to overcome during the application process. In one informational interview, I had to make 3 attempts to convince the person I was talking to that despite my degree being in neuroscience, I had no experience or interest in doing bench science at the company. I tried to address these issues by learning the appropriate language to use in resumes and interviews (which I will discuss in more detail later), but I am still working on the best way to position my PhD as relevant experience.

I also held misconceptions about the appropriate level at which to apply. A professional mentor had informed me that companies would consider my PhD as work experience and that I could apply to more senior positions. However, I discovered that this was only partially true. While some positions considered my PhD work as technical experience (i.e., X years of experience with machine learning models), it was not viewed as actual work experience (i.e. X years of experience as a data scientist). "Senior data scientist" positions typically require experience in a for-profit company, preferably one with a similar business model as the hiring company. The more realistic expectation is to begin with an entry-level data scientist position and advance to a senior level after demonstrating an ability to prioritize the company's interests. For some people this can happen quickly (in about a year).

Finally, I had a significant misunderstanding about what was expected from job application materials. My past experience with marketing myself was mostly through personal statements for school, which focused heavily on why I was interested in pursuing further education and why I was passionate about a particular program. However, I quickly learned that this approach did not work for job and internship applications. Instead of trying to convince employers of my commitment to a particular field, I needed to focus on showcasing what I could offer to their company. It became apparent that employers are primarily interested in how an applicant can be valuable to their organization, rather than why the applicant wants to work for them.

Informational interviews and networking

Almost every resource I found emphasized that informational interviews and networking was very important for landing the first job in a field. Unfortunately, I found this to be true. I had over 20 informational interviews during my PhD and job search. Some were at early stages when I was still figuring out what to do, and others were directly tied to specific job ads. While I love hearing about people's experiences, I am generally nervous to talk to them about it directly and prefer to gather perspectives from books and blogs. Overall, I found the process of informational interviewing quite taxing - however many of them gave me useful information or, in a minority of cases, a referral for a job.

There are a lot of resources available online for informational interviews. I also used my school's career center as a resource on this topic. Much of the advice on networking is tailored to different levels of familiarity, such as reaching out to a friend, an acquaintance, or a stranger.

An important note on LinkedIn: while academics do not rely on it, industry 100% does. I learned that to show up on recruiters' feed, you need to have some basic engagement with the app. I followed some popular pages like sklearn, pytorch, etc., and liked their posts to boost my visibility. I have no way of knowing if this was helpful.

In my search, I reached out to strangers very infrequently and instead relied on people I knew from school in one way or another. This approach was not recommended to me, but it is what I was most comfortable with. I was pleasantly surprised to learn that I passively benefited a lot from my undergrad and grad school's network. I had one interview that resulted from a referral from a friend, but all five others had team members that went to either my undergrad or graduate university. Even though I did not reach out to these people for informational interviews, I think I benefitted from baseline credibility that I gained from sharing an educational background. I think I was fortunate to have gone to schools with some name recognition that placed a lot of people in tech. This observation is what motivated me to so say that networking mattered for me. While most of my interviews weren't tied to me reaching out to someone at the company, all involved some kind of personal connection to my background.

At their best, informational interviews are great ways to get energized about a position and learn more about a job. They might even lead to referrals and eventually offers. I tried my best to embody this attitude as I reached out to people to network.

Internships

Of the individuals I know who moved straight from a neuroscience PhD to a data scientist role (n=3), all of them landed their first job by starting with an internship. There are similar paths through bootcamps and fellowships, but I do not have any experience with those. When I began exploring internship opportunities, I was not aware of how common it was for companies to hire interns from graduate school. I limited my search to 3 or 4 places where I had direct connections, but I later discovered that internship searches can be quite broad, with many opportunities available on platforms like LinkedIn.

Another noteworthy aspect of internships is that the expectations for them are different from those for full-time positions. Internship programs typically seek interns who can make meaningful contributions in a short amount of time, which makes it crucial to present oneself from the perspective of what one can offer. Companies are less likely to select candidates who require significant training. In contrast, when filling full-time positions, companies may be willing to invest in training to help a candidate gain skills if they are otherwise a good fit for the company. Additionally, some companies may even have less competition for full-time positions than internships.

Resumes and Cover Letters

When I first started applying for jobs, I sought help from my University's career center for guidance on crafting my application materials. At first, I found their advice to be very beneficial, and my application materials significantly improved. They helped me make more specific resume items, and told me to always customize my resume and always submit a cover letter. However, I eventually encountered conflicting advice from different advisors, leaving me unsure about which changes to make. Eventually, I realized that there was no "perfect" resume, and there would always be some element of chance involved in trying to appeal to the hiring manager.

When applying to large companies, it is common for your resume to be screened by a computer program that checks for your suitability for the job. These programs aim to match elements of your projects to the job description, although they can sometimes make egregious errors. To tailor my resumes to each position, I used a tool provided by my university called ResumeTargetted. This tool helped to identify key words and phrases to include in my resume to make it a better match for the job. If you don't have access to a similar tool, you can still try to use the language and terminology from the job ad in your application materials. I have no idea if this process of changing language was helpful or not, but I found it comforting to have some kind of formula to follow when making my resumes.

Interviews

By the numbers

Advancing through job interviews is a highly unpredictable process, and unfortunately, you have to go through many of them before knowing whether you're competitive. The rough rule of thumb I was given for full-time job applications was an application-to-interview ratio of 10 to 1. If you've applied to 20 jobs and haven't received any responses, it might be worth revisiting your application materials. However, if you've only applied to about 10 jobs, you might just have to keep at it for a bit longer.

Similarly, I was told that it takes an average of about 5 interviews to receive a job offer. If you're consistently getting stuck at a specific point (e.g. technical, behavioral), it's worth revisiting your approach. However, if you're making it to the final stages of interviews and not receiving an offer, it's likely just a matter of bad luck. If you persist, you will likely find something eventually. I found this easier said than done - the amount of rejection I faced was often devastating. I was grateful to have a strong support system and non-work activities to help sustain me.



For technical interviews specifically, many companies use services like LeetCode to generate questions. Many applicants spend a lot of time studying these. I purposefully avoided companies that used these services, and therefore have no insights on how to prepare for them.

Preparing

Another thing I learned while interviewing is that many companies expect candidates to fully understand their business model at the oustset and not to learn it on the job. During an interview with a healthcare startup, I gave a presentation on some analyses I had done on a subset of their data. My conclusion was that the company was underrepresented in an area that needed their service. Someone asked me how I would measure if my plan was successful for the business if enacted - a question I found very confusing. To me it seemed obvious: more people needing the service == more more people using the service == good for company. It turned out that this company mostly sells to other companies rather than people so my original logic does not pan out. If I had known this beforehand, I would have structured my proposal differently.

I'm still trying to figure out how to gain this knowledge reliably, but a few things have helped. For example, the website CrunchBase provides basic information on companies' finances and links to news and articles about them. You can also look for public earnings reports or quarterly updates that companies provide publicly. Additionally, exploring a company's website can sometimes provide clues about which customers are important to them and which new products they are focusing on.

Asking questions

Not all of this information needs to be figured out before the interview. Generally, asking questions about the financials of the company is encouraged, and not a taboo subject as I had thought. A friend who is a software engineer encouraged me to ask these types of questions to get a better understanding of the business. For start-ups, he suggested: (1) How much runway do you have? This basically translates to how long will you be able to pay me if the company doesn't get more funding? (2) When do you expect to be profitable? I asked this once and got an answer that started with 'Oof', but the question was still answered in good spirits. For public companies, he also encouraged me to ask any and all basic questions I had about the business model. Do you primarily sell to clinicians, hospital, or patients? What are your goals for this quarter? etc. Essentially, very few questions were actually off-limits, and I found that whenever I did ask questions about the business model or the company's future, my interviewers responded well. I never got the sense that interviewer thought I sounded unqualified based on the questions I asked.

Conclusions

When I have conversations with people about making a career change, they often ask me, "If there was one thing you wish you had done in your PhD that would have better prepared you for getting a data science job, what would it be?" I believe the one thing that would have helped me with this process was letting go of the idea that my career path was entirely within my control and that a smooth and linear path meant I had done everything "right." My PhD experience unexpectedly helped me in many ways, and many things I thought would lead to an "easy" job did not work out. I also had to take short-term steps that seemed like a step "backward" or "sideways" and trust that they would ultimately lead me to a more fulfilling place. Currently, I have found a career path that meets many of my needs and supports the flexible lifestyle I want in other domains. I fully expect that this may change again in the future. What I wish I had done during my PhD is internalize that all of these experiences are normal.

Other resources

These were some other resources I used during the job search that helped me appreciate the diversity and non-linearity or career paths out there.

• Build a Career in Data Science book and podcast
• Dr. Tanya Jonker's blog
• Dr. Lily Jampol put on the career event that I found most true to my experience

Double/debiased machine learning II: application

Application of the DML method to simulated data, with code, December, 2022

What is double/debiased machine learning?

Double or debiased machine learning (DML) is a method for estimating causal treatment effects from complex data [1]. In biomedical settings, treatment effects can tell you how much the administration of a given medication (T) can decrease the risk of some adverse event (Y) while accounting for other confounding variables (X). Essentially, it isolates the arrow connecting T to Y in the diagram below. At a population level, this value is called the average treatment effect (ATE), or \(\theta\). At the individual level, this value is called a heterogeneous treatment effect, conditional average treatment effect (CATE), or \(\theta(X)\) (the rest of this post will discuss CATEs rather than ATEs).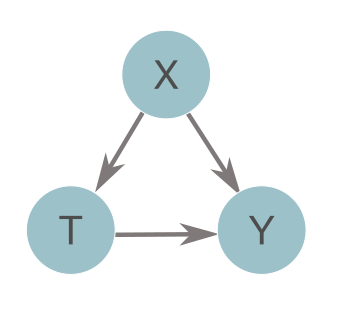 If causal assumptions are met [2], DML can provide us with accurate estimates of treatment effects, with confidence intervals, without making strict assumptions about the form of the data. The lack of strict assumptions is achieved by leveraging machine learning to estimate confounding effects (the X to Y and X to T arrows above). In short, the method estimates treatment effects with a 3 step algorithm:

1. Estimate the mapping from X to Y with ML
2. Estimate the mapping from X to T with ML
3. Regress the residuals from (1) onto the residuals from (2). The results of this is the treatment effect

If you want to learn more about the theory behind the method, check out my earlier post. If not, there are two features of this algorithms implementation that are important moving forward. First, the algorithm makes use of internal sample-splitting procedure, so training data have to be big enough to be split within the algorithm. The second is that Step 3 is solved in such way that the solution is robust to changes in Step 1 and Step 2. This mean that we find values of \(\theta(X)\) that are robust to changes in the Y and T models. This also means that the performance of your Y and T models do not have to be spectacular to achieve good estimates of the treatment effect. This second feature is something we're going to explore via a simulated example.

Data generating process

We're now going to walk through an example application of DML to a simulated dataset. We will use the following equations to generate our dataset: $$ {Y=T\times \theta(X)+\langle X| \gamma \rangle + \epsilon,} $$ $$ {T \sim Bernoulli( f(X) ), f(X) = \sigma( \langle X| \beta \rangle) + \eta} $$ $$ {\theta(X) = e^{2 \times X_1}} $$ Essentially, these equations are saying the Y is a linear combination of variables from X plus \(\theta\) times the treatment, and T is a binarized, linear combination of other variables from X. Lastly, \(\theta\) is an exponential function based on the first column of X. More specifically,

• Y the treatment effect times a binary indicator of treatment, plus a linear combination of variables from X, plus some noise. \(\gamma\) selects the and weights the columns of X included in the simulation.
• T is the binary treatment variable. It is calculated by passing a linear combination of variables from X, weighted and selected by \(\beta\), into a sigmoidal logit function \(\sigma\).
• \(\theta(X)\) is an exponential function of the first column of X times 2
• \(\gamma\), \(\beta\) have 50 nonzero elements, which are drawn from a uniform distribution between -1 and 1
• \(\epsilon\), \(\eta\) are noise terms uniformly distributed between -1 and 1
• X is a matrix with entries uniformly distributed between 0 and 1

Here, we want to simulate data that would make prediction of the CATE values more difficult so we can evaluate performance outside of best-case-scenarios. Therefore, we will simulate a situation with many correlated covariates (50) and many noise covariates (50). This paper [3] compares DML performance across different widths of X.

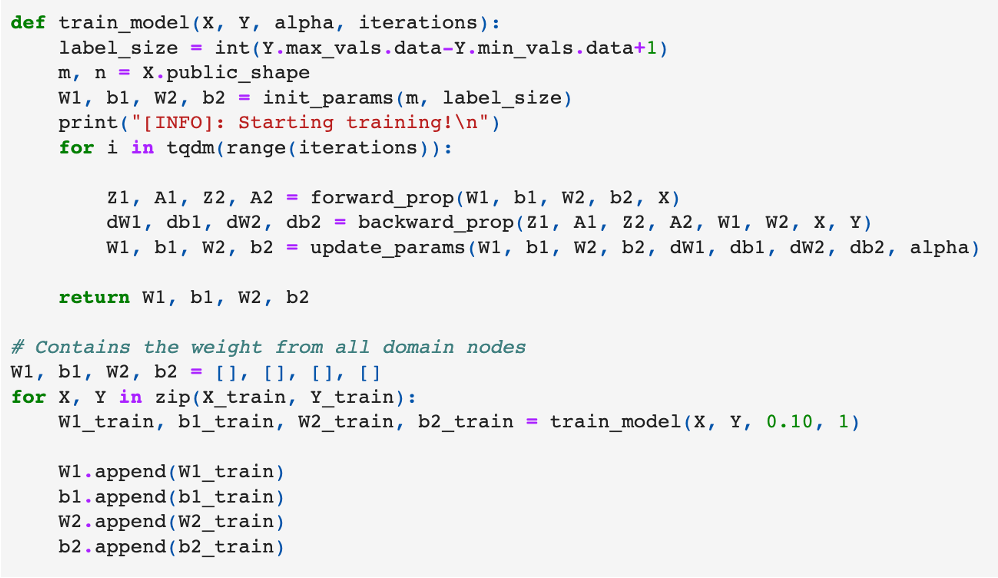
We can simulate our data in Python with the code below:

 
        import numpy as np

        def get_data(n, n_x, support_size, coef=2):
            """
            heterogeneous CATE data generating process
        
            params:
            :param bin_treat: a boolean indicating whether the treatment is binary (true) or continuous (false)
            :param n: the number of observations to simulate
            :param n_x: the number of columns of X to simulate
            :param support_size: the number of columns of X that influence T and Y. Must be smaller than n_x
            :return: x, y, t, and cate, the features, risk, treatment, and treatment effect
            """
            # patient features
            x = np.random.uniform(0, 1, size=(n, n_x))
        
            # conditional average treatment effect
            cate = [theta(xi, coef=coef) for xi in x]
            # noise
            u = np.random.uniform(-1, 1, size=[n, ])
            v = np.random.uniform(-1, 1, size=[n, ])
            # coefficients
            support_Y = np.random.choice(np.arange(n_x), size=support_size, replace=False)
            coefs_Y = np.random.uniform(-1, 1, size=support_size)
            support_T = support_Y
            coefs_T = np.random.uniform(-1, 1, size=support_size)
        
            # treatment
            log_odds = np.dot(x[:, support_T], coefs_T) + u
            t_sigmoid = 1 / (1 + np.exp(-log_odds))
            t = np.array([np.random.binomial(1, p) for p in t_sigmoid])

            # risk
            y = cate * t + np.dot(x[:, support_Y], coefs_Y) + v
        
            return x, y, t, cate 
        >

We can also explicitly define a function for \(\theta(X)\)

 
        def theta(x, coef=2, ind=0):
            """
            exponential treatment effect as a function of patient characteristics (x)

            :param x: the feature data for a single observation (size 1 x n_x)
            :param coef: the coefficient in the exponential function (default 2)
            :param ind: an integer indicating which column of x to use in the exponential function (default 0)
            :return: the treatment effect for a given observation
            """
            return np.exp(coef * x[ind])
        >

After simulating our data, we're also going to split off a test set from our data for evaluation. It's also important to remember that each training fold is going to be further split within the DML estimator, so we want to make sure there are enough observations in the training set to split further.

 
        n = 5000
        n_x= 100
        support_size=50
        x, y, t, cate = get_data(n, n_x, support_size, coef=2, bin_treat=True)
        x_train, x_test, y_train, y_test, t_train, t_test, cate_train, cate_test = train_test_split(x, 
                                                                                                    y, 
                                                                                                    t, 
                                                                                                    cate, 
                                                                                                    test_size=0.8)    
        >

The broad goal from this point will be to see if we can build a model that accurately estimates \(\theta(X)\). In the DML algorithm, this happens in three steps: (1) train a model for T; (2) train a model for Y; and train an estimator for \(\theta(X)\). We'll be using scikit-learn for the machine learning model, and econML for the DML estimator.

Train T model

You can really train your model however you want, we're just going to define a simple random forest model here. econML has the benefit of working with GridSearchCV objects and taking care of Y and T hyperparameter tuning for us (if you aren't familiar with GridSearchCV, check out its docs).

        from sklearn.ensemble import RandomForestClassifier
        from sklearn.model_selection import GridSearchCV
        
        # parameters for forest
        params = {
            'max_depth': [5, 10],
            'min_samples_leaf': [2, 4, 10],
            'min_samples_split': [2, 4],
            'n_estimators':[400, 1000]
            }
        
        t_mdls = GridSearchCV(RandomForestClassifier(),
                                params,
                                cv=5)
        t_mdl = t_mdls.fit(x_train, t_train).best_estimator_  
        >

We'll use ROC to see how well our T model is doing

 
        from sklearn.metrics import roc_auc_score, roc_curve
        import matplotlib.pyplot as plt

        # evaluate T
        import matplotlib.pyplot as plt
        
        pred = t_mdl.predict_proba(x_test)[:,1]
        
        fpr, tpr, _ = roc_curve(t_test,pred,drop_intermediate=False)
        roc_auc = roc_auc_score(t_test,pred)
        
        plt.plot(fpr, tpr)
        plt.plot([0, 1], [0, 1], color='navy',linestyle='--')
        plt.xlabel('False Positive')
        plt.ylabel('True Positive')
        >

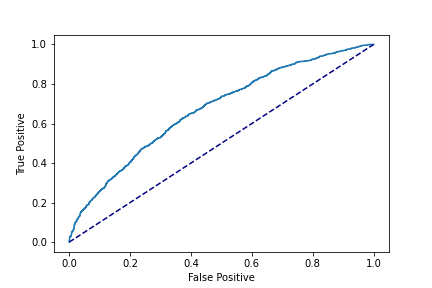
print(roc_auc)

Output:

            0.6471481
            

Our T model AUC is 0.65, which is far from impressive. But remember, we can (theoretically) get good CATEs even if our T model performance isn't great, so let's keep going.

Train Y model

We can do the same thing for the Y model. Let's use a gradient boosted classifier to mix things up.

 
        # fit y
        from xgboost import XGBRegressor
        
        # parameters for forest
        params = {
            'max_depth': [5, 10],
            'learning_rate': [0.1, 0.01, 0.05],
            'n_estimators':[50, 400, 1000]
            }
        y_mdls = GridSearchCV(XGBRegressor(),
                                params,cv=5,
                                n_jobs=-1)
        
        y_mdl = y_mdls.fit(x_train, y_train).best_estimator_
        >

For the continuous variable, we will evaluate our performance by calculating the bias, or the percent deviation from the true estimate.

 
        # evaluate Y
        pred = y_mdl.predict(x_test)
        
        plt.scatter(pred, y_test)
        lims = [
            np.min([pred, y_test]),  # min of both axes
            np.max([pred, y_test]),  # max of both axes
        ]
        plt.plot(lims, lims, color='navy',linestyle='--')

        plt.xlabel('Predicted Y')
        plt.ylabel('True Y')
        >

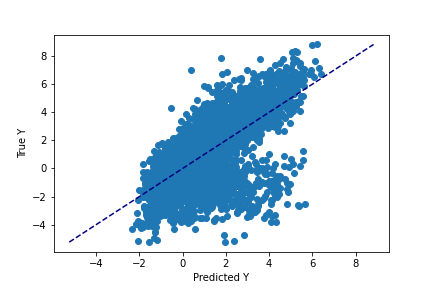
np.mean(np.abs(pred - y_test) / y_test)

Output:

            0.4681890
            

Similarly, we get mediocer performance when estimating Y. Our values have a bias of about 47%, meaning that if our true Y value was 10, our model would be guessing 15.

Train the estimator

We can now pick an estimator. econML has 3 main estimators that provide confidence intervals. The 'SparseLinear' and 'Linear' estimator will only work if you have many more observations than variables (see this table for comparisons of different estimators). For a lot of real-world data, this is not the case, therefore we will use the last remaining option: CausalForest estimator [4]. Like random forest models, this estimator also has the benefit of being able to estimate non-linear treatment effects in a piece-wise fashion.

 
        # dml
        from econml.dml import CausalForestDML
        
        est = CausalForestDML(model_y=y_mdl, model_t=t_mdl, cv=5)
        >

This function takes care of the sample splitting procedure! The argument 'cv' defines how many folds to use for cross fitting. The default is 3, but the original paper recommends using 5 or 6 if possible.

Also similar to 'RandomForestClassifiers' in scikit learn, the 'CausalForest' estimator has many other parameters. If you're familiar with random forests many of these parameters will be familiar: the number of trees to include, the maximum depth of those trees, etc. The big exception in parameters between causal forests in econML and sklearn is that econML forest has no class weighting option. This is because the causal forest method makes use of a specific weighting strategy already [4].

Additionally, the econML estimator can't be used as input into sklearn's 'GridSearchCV' or 'RandomSearchCV' functions. However, we can use econML's own hypterparameter tuning function 'tune'. Rather than evaluating parameter performance across cross-validated folds of data, this fucntion uses out-of-bag scores on a single, small forest.

 
        # parameters for causal forest
        est_params = {
            'max_depth': [5, 10, None],
            'min_samples_leaf': [5, 2],
            'min_samples_split': [10, 4],
            'n_estimators': [100, 500]
        }
        est = est.tune(Y=y_train, T=t_train, X=x_train, params=est_params)
        

Our estimator now has tuned parameters, but it still needs to be fit.

 
        est.fit(Y=y_train, T=t_train, X=x_train) 
        

That's it! Now we can look into evaluating how well we did.

Evaluation

Before we evaluate the model performance, we're going to talk about viewing individual CATEs and their confidence intervals. In a clinical application, these values are what would be used in the decision-making process surrounding which interventions to use for a given patient.

 
        # get individual CATES
        patient_idx = np.random.randint(np.shape(X_test)[0])
                
        # get cate
        cate = mdl.effect(X_test[patient_idx:patient_idx+1,])[0]
        
        # get cate CI
        lb, ub = mdl_dict[name].effect_interval(X_test_clean[patient_idx:patient_idx+1,], alpha=0.05)
        
        # plot CATEs with CI for individual patients
        plt.figure(figsize=(8,6))
        plt.errorbar(1, cate, yerr=ci, 
                        fmt="o", ecolor='k', zorder=1)
        plt.tight_layout()
        >

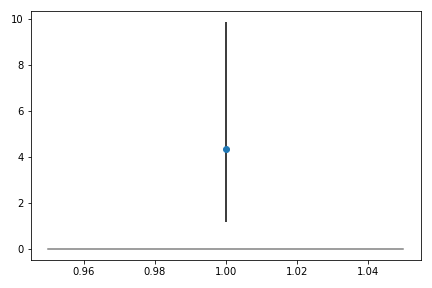This plot indicates that for this patient, the model estimates that adding the treatment will increase the outcome measure by 4, though it has a wide confidence interval, spanning about 1 to 10.

Now we can move on to evaluation. How'd we do? Since this is simulated data, we can see how well our estimated treatment matches the true effect.

 
        # plot 
        plt.figure()
        plt.scatter(x_test[:,0], cate_test, label='True Effect')
        plt.scatter(x_test[:,0], cate_pred, color='orange', label='Predicted Effect')
        plt.xlabel('Patient Features')
        plt.ylabel('CATE')
        plt.legend()  
        >

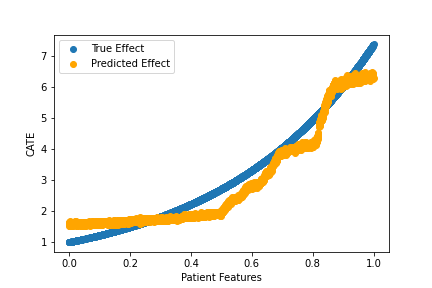
np.mean(np.abs(cate_pred - cate_test) / cate_test)

Output:

            0.1577856
            

We did pretty well! Notably, we did pretty well even though our T and Y models had mediocre performance. Here our model bias is about 16%, substantially lower than the bias for Y. What are the limits of this good performance though? What is the minimum number of samples? What happens when we add more variables, or more noise? This paper [3] shows that DML (and all causal estimation methods) do better with more samples, fewer variables (though DML does better than other methods when the number of columns of X > 150), fewer confounding variables, and weaker confounding.

Evaluations with empirical data

We can use simulations to demonstrate that DML can perform pretty well in some messy situations - like when we get mediocre predictions of T and Y. However, all these demonstrations rely on the fact that we know the true value of \(\theta(X)\). In real-world settings, this is not realistically possible, so how do we evaluate our models? I've been exploring a few options:

• Consistency in CATE and ATE estimates: While this method is more of a validity check than an evaluation, it is considered best practice for any method estimating conditional average treatment effects (CATEs, which were the subject of this post). The idea is that you bin your heterogeneous treatment effects into a few bins and recalculate average treatment effects within each bin. While we didn't discuss them here, average treatment effects (ATE) are a sample level equivalent of the conditional averages. If your ATE and CATE distributions are similar, you can have more confidence that your CATE estimates are not spurious.
• Benchmarking and medical knowledge: To some extent, we can leverage medical knowledge to confirm that our CATEs are in the right neighborhood. For example, we have substantial scientific evidence that aspirin can lower people's risk for heart attack. Therefore, if our mean CATE is ~20%, indicating an increase in risk, we can be reasonably sure that the model isn't performing well.
• Improved prediction: we can also put the evaluation back into a prediction-based framework. Mathematically, a patient’s true risk Y(t) = Y(t-1) + CATE. If our predictions get better with the addition of the CATEs, we can at least conclude that our prediction is useful. It’s important to note that 'useful' is not the same as 'accurate’ and is not a validation of the causal assumptions of the model.

References

1. Chernozhukov, V., Chetverikov, D., Demirer, M., Duflo, E., Hansen, C., Newey, W., & Robins, J. (2016). Double/Debiased Machine Learning for Treatment and Causal Parameters. http://arxiv.org/abs/1608.00060
2. Rose, S., & Rizopoulos, D. (2020). Machine learning for causal inference in Biostatistics. In Biostatistics (Oxford, England) (Vol. 21, Issue 2, pp. 336–338). NLM (Medline). https://doi.org/10.1093/biostatistics/kxz045
3. McConnell KJ, Lindner S. Estimating treatment effects with machine learning. Health Serv Res. 2019 Dec;54(6):1273-1282. doi: 10.1111/1475-6773.13212. Epub 2019 Oct 10. PMID: 31602641; PMCID: PMC6863230.
4. Oprescu, M., Syrgkanis, V., & Wu, Z. S. (2018). Orthogonal Random Forest for Causal Inference. http://arxiv.org/abs/1806.03467

Federated learning for clinical applications

A primer for the data-governance/privacy curious, October, 2022

Data Privacy and Governance in Clinical Machine Learning

Clinical machine learning seeks to ethically improve patients’ outcomes in healthcare settings using complex data and statistical methods. Generally, many of these statistical methods involve learning associations between various real-world measures – like the risk of disease X and the amount of protein Y. The accuracy of these learned associations tends to increase as you get more data. Additionally, newly developed methods with the potential to solve unique problems, also tend to require more data to get accurate results. Likewise, models targeting rare conditions require, unsurprisingly, even more data. This is not to say that data is the only issue facing clinical machine learning, but it certainly an important factor in the field's progress. However, the process of collecting storing, and distributing data, especially medical data, is extremely difficult and often not incentivized. We’re going to briefly discuss two important aspects of the data ecosystem -- data privacy, and data governance. We’ll then describe a technical advancement in model training – federated learning – that allows for model development in an ecosystem focused on maintaining decentralized data governance [1].
Data Privacy: Medical data are often highly sensitive in nature and breaches in privacy could cause significant harm to patients. Additionally, it is becoming clear that simply anonymizing data – i.e. removing patient names and unique identifiers – might not be enough to ensure privacy. We now know that patient faces can be reconstructed from medical scans, making the patient's identifying features and the features used in modeling inseparable in these applications[2]. These issues make hospitals hesitant to share data, even with other hospitals, and put high security requirements on any server seeking to host shared data from multiple sources.
Data Governance: Collecting, storing and maintaining large datasets takes massive amounts of work. In academic settings, providing these datasets as a resource to the public is not incentivized; time spent writing original research papers is considered more useful. Similarly in industry or non-profit settings, institutions often want to retain control of their data efforts because of the resources invested into them. While it would also benefit progress to incentivize sharing, finding ways to work within current incentive structures for data governance can help build larger multisite datasets quickly.
Both data privacy and data governance are necessary parts of the data ecosystem that unfortunately disincentivize institutions to share their data or contribute them to larger data lakes. Making them both an important safeguard and a barrier to progress. If there were a way to decentralize model training such that institutions could retain control of their data, and modelers could incorporate that data into their work, clinical applications could advance without sacrificing privacy or drastically changing incentives. This decentralization is the promise of federated learning.

Federated Learning Definition

Federated learning achieves decentralization by training individual models at each participating institution and then aggregating the parameters from each local model to create one global model. This way, data are never passed between sites, only parameters are. Before going into a bit more depth on the definition, lets visualize a typical centralized learning pipeline (visuali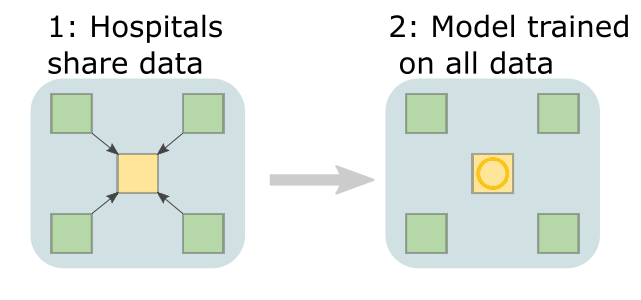zation adapted from [1]). Data from multiple hospitals (green squares, called 'nodes') would need to be shared with some central server (yellow square, called 'aggregate node' or 'central node'). Assuming that was successful, you could then train a model on data from every site at that centralized server. Seems simple, but we’ve already discussed why data sharing might not be a sustainable solution. Let instead look at the schematic for federated learning (visualization adapted from [1]). 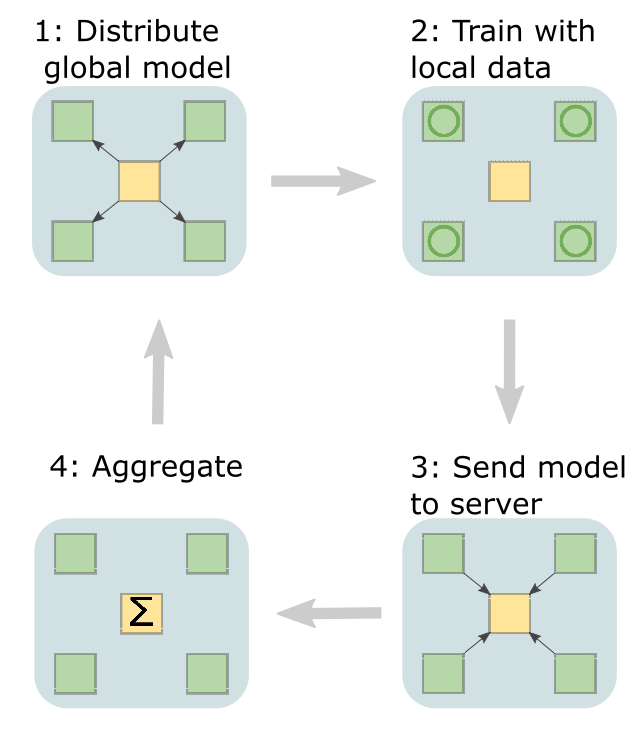The first step is for the central server to share a model with each node. Then, models are trained locally before sending their parameters back to the central server. The central server will then aggregate all the parameters, before sending the updated model back out to each hospital. This repeats until the model is trained. To formalize this definition, let’s think about a standard loss function from a machine learning model. $$ \min_{\phi} L(X;\phi)$$ Typically, the goal is to minimize some loss function \(L\) over different parameters \(\phi\). Now, we can expand this loss function to accommodate a decentralized framework $$ L(X;\phi) = \sum^{K}_{k=1}w_k L_k(X_k;\phi_k) $$ Here \(k\) indexes each local data source. Now, we are simply minimizing the weighted sum of local losses. Typically, this weighting \(w_k\) is given by the fraction of observations present at each hospital, but different weighting schemes can serve different purposes (more on this later). It’s important to note that federated learning is huge field, with lots of different flavors and variations. What was described above, and what will be discussed in the remainder of this post is a specific kind that seems natural to many clinical applications. Specifically, these applications involve aggregating data from multiple hospitals, such that each node is a hospital, and each hospital stores mostly the same variables. To facilitate future searches, this method is called centralized federated learning (which is confusing, given that the alternative to federated learning is called centralized learning), using the FedAvg algorithm with a hub and spoke topology.

Decisions and Considerations when Implementing Federated Learning

Before implementing any federated learning system, there are some precursor decisions you’ll have to make, as well some features of your data that should be quantified. Some of these decisions have standard solutions for the generic medical context (i.e. multiple hospitals, with mostly the same features, but different observations). For the few considerations that don’t have standard solutions, we’ll go over a set of common options in more detail.

Decision or Consideration	Description	Standard Solution in Clinical Setting
Nodes and Topology	How many nodes? Will there be aggregate nodes? How will they be connected?	Few nodes (each node is a hospitals), all connected to one aggregate
Updates	How many nodes will participate in each update?	All connected nodes will participate in updates
Data structure	Naming conventions, file structures, etc.	None, because it depends so much on the specific problem you’re working with. Here’s an example from neuroscience called BIDS
Data partitions	Are features, labels, or observations shared across nodes?	Each node will have different observations, but at least some shared features and labels
Data distribution	How are features and labels distributed across nodes, and how will this influence the learning algorithm?	Multiple (see below)
Privacy measures	What extra privacy measures will be taken, if any?	Multiple (see below)
Hyper parameters	Weighting coefficients (wk), loss function, etc.	Weighting by the number of observations, but there are some interesting and useful variants (see dealing with non-IID data for some examples). All other parameters determined similarly to centralized learning

We will discuss the two issues with multiple solutions: data distribution (specifically, non-independent, or non-IID data); and additional privacy.
Dealing with Non-IID Data: The biggest technical issue on this list is probably 'data distributions'. The standard FedAvg algorithm discussed here is not guaranteed to work well when the data are not identically distributed (non-IID) across nodes – and is rarely IID across nodes in real-world settings. Quantifying how the distributions of data differ and adapting the algorithm to deal with those distributions is an important part of the process. Overall, there are three big ways that data can differ across nodes. Nodes can have missing values, nodes can have different distributions or proportions of values, or the same values can lead to different predictions in different contexts. When reviewing the literature, it seems like each of these different data situations has a unique name, however not everyone seems to agree on what that name is. I think you can understand everything in this post without the names, but for the purpose of searching the field, here are the common names I observed for these different data situations:

1. Feature skew: some features not present. i.e. one hospital does not record heart rate.
2. Label distribution skew: some labels are not present. i.e. building a model to predict COVID when one hospital has no patients with COVID.
3. Concept Shift: the same features lead to a different label. i.e. building a model to predict gut health from cheese consumption with hospitals in Asia and Europe. Since lactose intolerance is more common in Asia, the 'cheese' feature would lead to different labels at different hospitals
4. Concept Drift: or the same label arises from different features. i.e. building a model to predict anxiety levels in hospitals with patients from different socioeconomic levels. While both hospitals might have patients with anxiety, the things causing that anxiety might differ.
5. Quantity skew: labels have different distributions (imbalanced). i.e. building a model to predict COVID when one hospital has 40% of patients test positive, and another has 2%.
6. Prior probability shift: features have different distributions. i.e. using age as a predictor when data come from children's hospitals and general hospitals.
7. Unbalancedness: vastly different numbers of observations. This one is self explanatory.

A survey of clinical applications of federated learning before the year 2022 quantified how many papers reported each of the first 5 distributions above. The most common distribution reported was quantity skew, or imbalanced labels across nodes (18/24 papers)[3]. Because of its ubiquity, we’re going to go over some common solutions as well.

1. Balancing training data: each node can implement its own resampling scheme, such as SMOTE or GAN resampling. In the same review mentioned above, this was the most popular method for addressing skew [3], though the review only discussed the first three methods in this list.
2. Adaptive hyperparameters: using loss functions and weighting coefficients that are specific to each node.
• LoAdaBoost: one specific example that boosts the training of weak nodes by forcing the loss function to fall below some threshold before they contribute to the aggregate[4].
3. Domain adaptation: Use meta-training to determine how to combine predictors trained on various domains, similar to transfer learning[5].
4. Share data: share a small amount of data or summary statistics from data to fill in missing values and supplement skewed distributions
5. Normalization: (only applied to deep learning models) group, rather than batch normalization helps with skewed labels[6].
6. Different algorithm: Federated learning based on dynamic regulation (FedDyn) algorithm can guarantee that the node losses converge to the global loss[7].

Dealing with Privacy: Despite federated learning being more secure than centralized methods, federated learning is not free from privacy risks. Bad actors with access to the model can still reverse engineer data from the model parameters, and therefore gain access to sensitive information. This issue is more pressing when not all the nodes can be trusted – like when nodes are users cell phones rather than hospitals. Because of this, about half of clinical federated learning papers do not use additional privacy protections[3]. However, if you’re interested in adding extra security, there are two ways that people tend to increase security: adding noise, and encryption.

1. Add noise: add noise to either the data, or the gradients
   • Differential privacy: a method of adding noise that ensures that model outputs are nearly identical even if any one data point is removed.
2. Encryption: encrypt the gradients or parameters that get sent back and forth

Python Packages for Implementing Federated Learning

If you’ve thought about the design of your federated learning pipeline and are ready to implement it, there are a few free packages in Python that can help you get your system up and running

1. PySyft
   A screenshot from a PySyft tutorial
   • Supports encryption and differential privacy
   • Support for non-IID data (via sample sharing)
   • ‘numpy-like’ interface (their words)
   • Currently, they want users to work with the team on new applications
2. Tensorflow
   A screenshot from a tensorflow tutorial
   • Probably easy to use if you already work with tensorflow
   • No built-in support for privacy or non-IID data
3. FATE
   A screenshot from a FATE tutorial
   • No support for non-IID data (though nothing is stopping you from adding your own resampling function to the pipeline)
   • Supports encryption
   • Pipeline package interface

Conclusions and Commentary

• Federated Learning promises a flexible, decentralized way to train machine learning algorithms. Widerspread adoption of federated learning could make modeling with more sophisticated methods, or for more niche populations feasible
• Federated learning is presented as a solution to data governance and privacy issues that make sharing data difficult. While the method has clear benefits over centralized learning, data privacy, and especially data governance, will likely still present issues moving forward. As discussed in the post, federated learning applications are not a complete solution to security issues and will likely require more protections in any real-world application. Additionally, the incentives that make it harder for institutions to contribute data to data lakes might also make it harder to offer access for federated learning projects. If you spent a lot of money collecting a rare dataset, you might want to get the first (or second, or third) crack at any modeling projects using that dataset. Essentially, I do not think federated learning can serve as a substitute for incentivizing data sharing or protecting/compensating data curators.
• Starting a federated learning project requires many decisions and considerations. Decisions with the least clear solutions are those involving data standardization across sites and those involving how to deal with non-IID data distributions. Both reviews cited in this post recognize that these are important issues[1,3], but stop short of providing clear recommendations. I think the method would be more accessible and more likely to be used responsibly if some of the packages produced pandas-profiler style reports of data distributions across sites and provided more support for implementing solutions.

References and Resources

1. Rieke, N., Hancox, J., Li, W., Milletarì, F., Roth, H. R., Albarqouni, S., Bakas, S., Galtier, M. N., Landman, B. A., Maier-Hein, K., Ourselin, S., Sheller, M., Summers, R. M., Trask, A., Xu, D., Baust, M., & Cardoso, M. J. (2020). The future of digital health with federated learning. Npj Digital Medicine, 3(1).
2. Schwarz, C. G., Kremers, W. K., Therneau, T. M., Sharp, R. R., Gunter, J. L., Vemuri, P., Arani, A., Spychalla, A. J., Kantarci, K., Knopman, D. S., Petersen, R. C., & Jack, C. R. (2019). Identification of Anonymous MRI Research Participants with Face-Recognition Software. New England Journal of Medicine, 381(17), 1684–1686.
3. Prayitno, Shyu, C. R., Putra, K. T., Chen, H. C., Tsai, Y. Y., Tozammel Hossain, K. S. M., Jiang, W., & Shae, Z. Y. (2021). A systematic review of federated learning in the healthcare area: From the perspective of data properties and applications. In Applied Sciences (Switzerland) (Vol. 11, Issue 23). MDPI
4. Huang, L.; Yin, Y.; Fu, Z.; Zhang, S.; Deng, H.; Liu, D. LoAdaBoost: Loss-based AdaBoost federated machine learning with reduced computational complexity on IID and non-IID intensive care data. PLoS ONE 2020, 15, e0230706.
5. Guo, J., Shah, D. J., & Barzilay, R. (2018). Multi-Source Domain Adaptation with Mixture of Experts
6. Hsieh, Kevin; Phanishayee, Amar; Mutlu, Onur; Gibbons, Phillip (2020-11-21). The Non-IID Data Quagmire of Decentralized Machine Learning". International Conference on Machine Learning. PMLR: 4387–4398.
7. Acar, Durmus Alp Emre; Zhao, Yue; Navarro, Ramon Matas; Mattina, Matthew; Whatmough, Paul N.; Saligrama, Venkatesh (2021). Federated Learning Based on Dynamic Regulation
8. For a lighter read, check out this comic from Google

Coastal differences in artists' Instgram captions

A network analysis of tattoo pieces, September, 2022

To me, tattoos seem like a great way to express autonomy, aesthetics, and interests all in one place. I'm always interested in hearing peoples tattoo stories, and my Instagram feed is usually about 70% images of fresh ink on any given day. Recently I've wondered what sorts of stories I might be missing by limiting my exposure to hyper-curated algorithms and people I already know. In short, I wanted to do a broader survey of the tattoo landscape. If I could pull enough data and do some statistical clustering, I could potentially sort through a much larger swath of the tattoos than I would normaly be exposed to. Specifically, I wanted to answer a few questions: What are the most common tattoo styles and subjects? How do these differ geographically in the US? If I can get descriptors of each tattoo, what are some prominent groupings of tattoo descriptors? Do those groupings differ in different cities? And, are there any interesting groups I haven't been exposed to so far? I decided to use Instagram posts to collate a dataset of tattoos, and to use hashtags from each post as markers of style, content, or other tattoo features. As a simple assessment of geographic specificity, I pull two datasets: one from San Francisco (SF) and one from New York (NY). I use these datasets to create a network representation of tattoos in each city. The network representation stores relations between posts and hashtags and allows me to identify clusters of similar posts and their content.

Common tags in SF and NY

From Instagram, we can get the top 10,000 posts from a specific hashtag (i.e. #sftattooartists, or #nyctattooartists). Each post has some information associated with it - the number of likes, the account that posted it, the hashtags, etc. Here we're going to throw out all this information except the hashtags. We now have bunch of posts, and all the tags used to describe them. Below, you can see the number of posts associated with the most popular hashtags. San Francisco tags are in cool colors, and New York tags are in warm colors.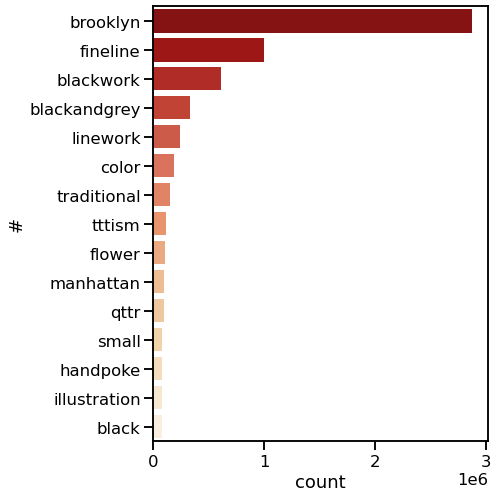

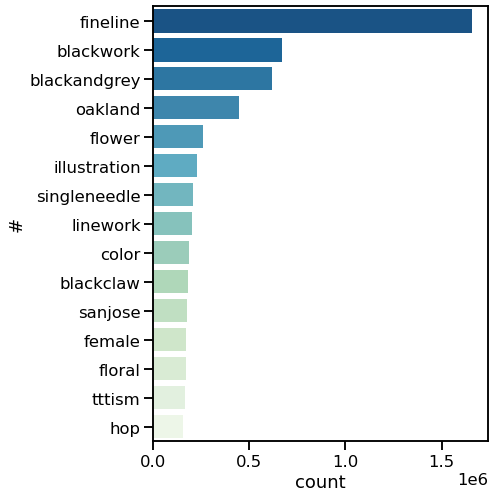
A lot of the popular tags break down into a few categories.

• Artist location: Artists include hashtags for nearby locations such as #brooklyn or #sanjose. These tags were probably originally something like #brooklyntattoo or #sanjosetattoo artist that got clipped in the hashtag cleaning process. It is also possible artists are making tattoos of these actual regions, though I think this is less likely.
• Tattoo subject: In both cities, flowers are a popular subject for tattoos (#floral, #flower), though this is the only subject the cracks the top 10.
• Tattoo style: A few styles like #fineline, #blackwork, #color and #blackandgrey a top tags in both cities. A few styles that are considered popular but don’t make the cut in both would be #traditional, #newschool, #japanese, etc.
• Tattoo magazines:
One tag, #tttism, is a tattoo magazine with a large digital division

One notable omission to me was hashtags about tattoo locations. While there are clearly more popular tattoo placements (#wristtatoo vs #facetattoo), no placements end up in the top 10. This is likely because many posts include a mixture of finished pieces and artwork that could theoretically end up anywhere. What about the biggest differences between cities? Below, we see the difference in the percentage of posts containing each tag, for each city.

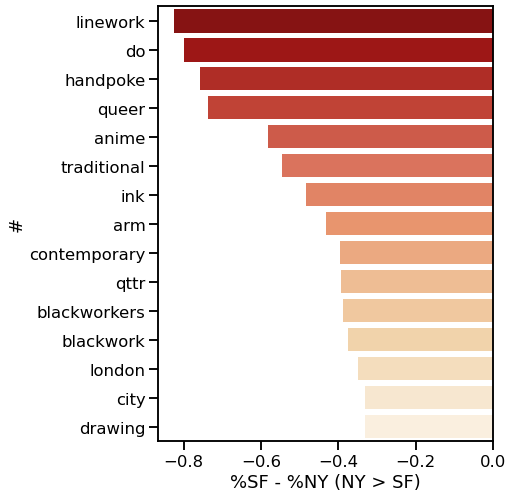
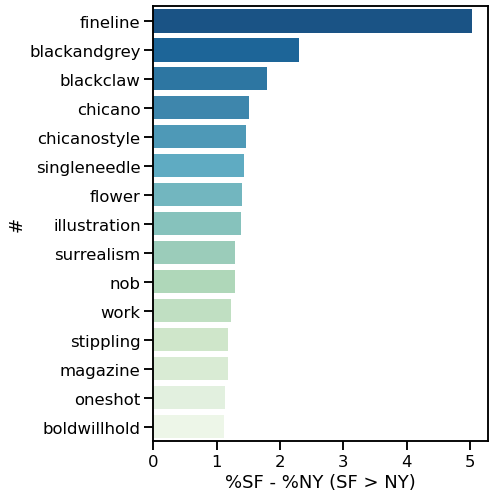
These separate into different categories.

• Artist identity: New York has a higher prevalence of both #queer and #qttr (which is an abbreviation for queer tattoo artist). Does this mean that there are more queer artists in New York? There are a few possible explanations. It is possible that there are more queer artists in NY, that queer artists in NY are more willing to self identify on social media, or that queer SF artists use different or more specific terminology.
• Tattoo techniques: One surprising difference to me was the prevalence of tags referencing different tattoo equipment on different coasts. Specifically, #handpoked tattoos, which are non-electric, are more popular in NY, while #singleneedle tattoos, which use only one kind of needle, are more popular in SF
• Tattoo style: One of the most interesting differences to me is the dichotomy between #traditional and #surrealist style tattoos on each coast. Surrealism constitutes a more niche style than traditional tattoos in general, and its prevalence in SF evokes images of the cities free-spirited, pre-silicon valley past for me. Similarly, #chicano and #chicanostyle are not often in listed in the US's top styles, but their growing popularity in a state with growing Latinx population seems intuitive.
• Tattoo subject: We find that NY has a much higher prevalence of anime tattoos compared to SF. However, it is once again possible that SF tattoo artists simply use different, or more specific language to tag their anime tattoos.

We've learned a lot about the coastal tattoo landscape just from looking at popular hashtags. But there is higher level information that this technique ignores. Which tags tend to be grouped together? What subjects, styles, and placements? To answers these questions about groups of descriptors, we are going to move on to our network analysis.

Instagram tattoo posts as networks

We can represent all the Instagram posts and their hashtags in a network like the one below. Nodes in this network are both posts (shown on the left), and tags (shown on the right). Lines connect posts to their corresponding tags.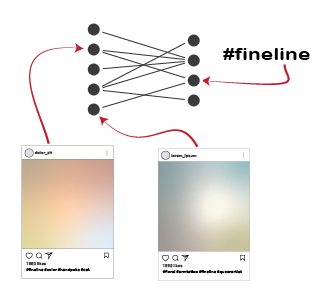 If you want to know how to make a network like this using Python, you can see the code here. To find groups in graphs, we are going to use a method that assigns distances to items based on how similar their connectivity is. So, two posts with the same hashtags would have a small distance, and posts with very different hashtags would have a large distance. We can then group the posts and hashtags such that distances are small within a group, and big between groups. But how many groups do we pick? If the best grouping gives us 10,000 groups is that useful? Rather than picking a specific number of groups, we're going to use a nested approach. This means that we're going to start with big groups, then look for smaller groups within those big groups, and repeat this process until our groups are very small. We will end up with a gradient of grouping descriptions that range from coarse-grained (few, large groups) to fine-grained (many, small groups). This way we can pick the resolution that suits our current questions best. Specifically, we're going to use a method called the nested weighted stochastic block model, that makes very few assumptions about the structure of groups and works especially well with big data. Below, we can see the network visualization of our two tattoo post networks. The left hand side shows posts, and the right hand side shows hashtags. The colors correspond to the different groups (at the most fine-grained level). You can also see the hierarchical structure of the nested groups overlayed on top in light blue.

Network clusters of tattoo posts

New York

San Fransisco

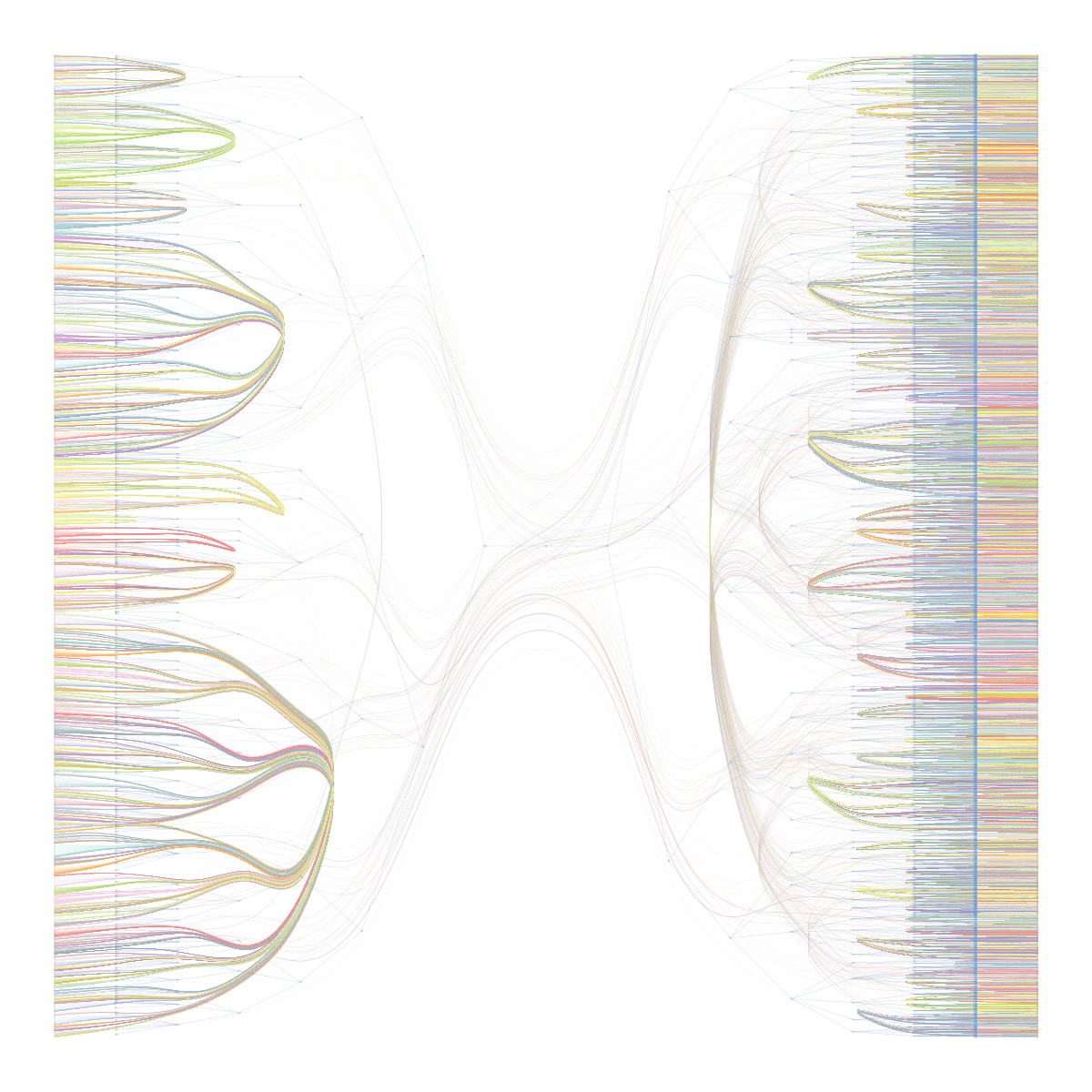
There are some prominent differences between the grouping structure of the two cities.
Nested CLusters in New York

1. Level 1: 2 groups
2. Level 2: 3 groups
3. Level 3: 7 groups
4. Level 4: 20 groups
5. Level 5: 52 groups
6. Level 6: 160 groups
7. Level 7: 637 groups
8. Level 8: 28282 groups

Nested Clusters in San Fransisco

1. Level 1: 2 groups
2. Level 2: 5 groups
3. Level 3: 14 groups
4. Level 4: 32 groups
5. Level 5: 98 groups
6. Level 6: 263 groups
7. Level 7: 1463 groups

New York has more levels than San Francisco, though the number of groups per level grows faster in San Francisco. Additionally, we find that the grouping in NY is 'better', meaning that within/between group distance separation is larger. This suggests a slightly less fragmented Instagram tattoo post landscape in New York, where smaller numbers of groups give the best distance separations. We can now pick a level with relatively few groups (Level 4) and visualize the different hashtags in each group. If hashtags are in the same group, that means that there is some overlap in the posts containing those tags. In the plots below, we can make word clouds to represent each group in level 4. The size of the word indicates the number of posts in the group that have the hashtag, and the size of the word cloud indicates the total number of posts in the group. The color indicates nothing, it's just for readability.
Hashtags in New York

Hashtags in San Fransisco
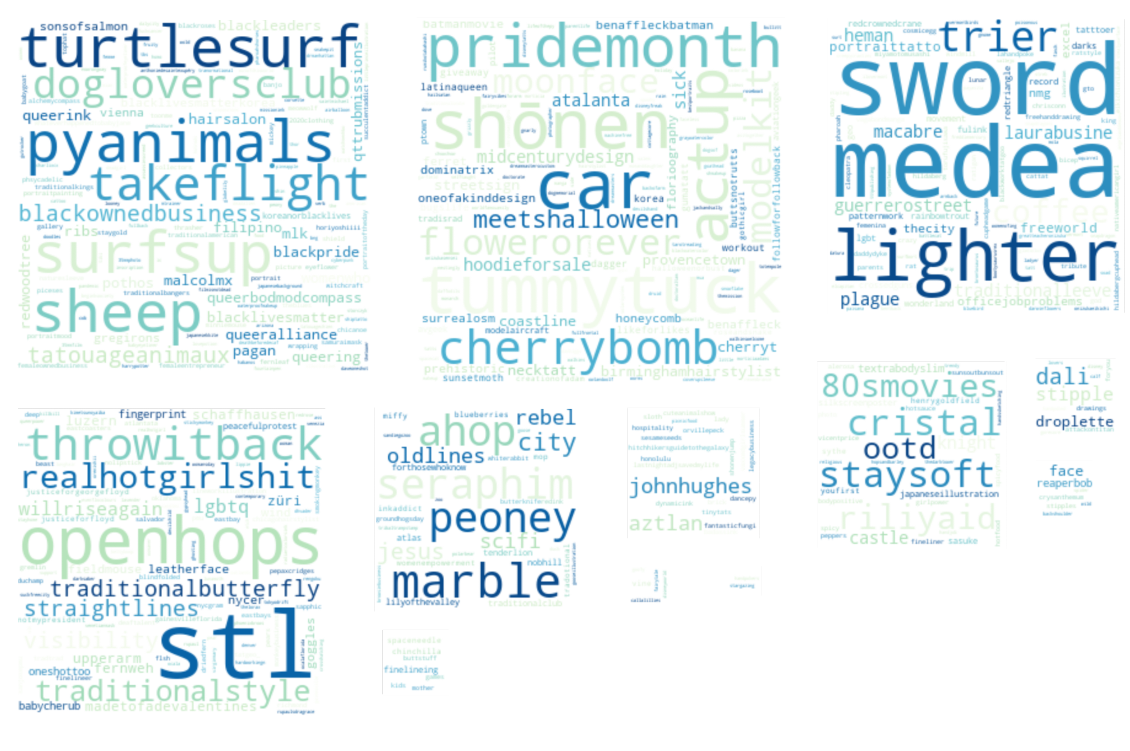
We can also see some interesting differences in this visualization. New York has communities that are more evenly sized, while San Francisco has are more small groups. Lastly, we can look at a finer scale and visualize the hashtags contained in some of the smaller communities.
We get some communities that are expected:

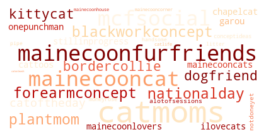
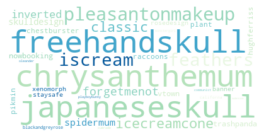
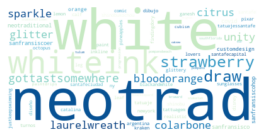
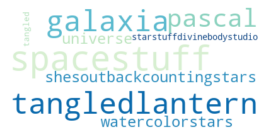
Others that are less expected, but show consistent themes:

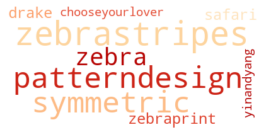
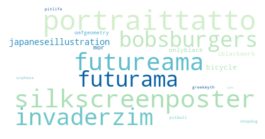
And lastly, some that show some confusing and inspiring mixes of topics:

Conclusions

• We find that regardless of city, fine line, black work, and black and grey styles are popular to tag. Similarly, flowers or floral designs are consistently mentioned
• San Francisco has a uniquely large community of artists posting about Chicano style and surrealist tattoos, while New York has more posts about anime tattoos and traditional styles
• We find some evidence that New York tattoo posts more easily separate into large groups, while San Francisco tattoos have more small, niche groups.
• A nonzero number of people have tattoos of the Ben Affleck batman

I do think I'm leaving this project with a better understanding of the tattoo landscape, at least as it is represented on Instagram. I've also learned how to work with a rich representation of transient cultural attitudes and am looking forward to finding some other fun applications of the method.

How many roads must a random walker walk down before it gets out of Reykjavik?

Analyzing your Google location history and biased random walkers on street graphs (in Python), August, 2022

I spent a good part of my PhD learning about how people explore spaces. I specifically was interested in abstract spaces, where distances in these spaces map on to the similarity between items. These items could be emotions, objects, school subjects, birds, or anything else you want. It turns out lots of the theories for how how humans learn and explore abstract spaces also hold water when examining how we or other animals explore physical spaces. These cross domain theories felt very satisfying to me; it seemed like they might at best be revealing something important about our behavior, and at worst showing cool convergent behavioral motifs. I wanted to take some of my knowledge of exploration, as well penchant for learning new data vis methods, to learn something about my own exploration style through physical space. What sorts of cost functions might I have in mind when traveling? How well have I really explored my city? How much are my paths driven by novelty, or familiarity? This blog post will answer none of these questions. But it will go through the steps I took to learn a few things that are fundamental to answering them: the structure of Google maps location data; and how to analyze road networks and implement random walks in Python. Along the way, we'll answer a much simpler and more pointless question: does my vacation to Iceland bear any qualitative similarity to a biased random walker?

Google location data for exploration

I'm going to use my own Google location data to visualize my path through Iceland. I followed these steps to download the data. The data come in two sets, a more information rich folder called Semantic Location History, and sparser json file called Records. We're working with only the Records data here. The important features of this data are latitudes and longitudes, as well as time stamps. Coordinates will be mapped to publically available road networks using the package OSMnx, and timestamps will be used to order and filter data. We can get rid of all the extra columns and clean up the ones we want like so:

            import pandas as pd
            import json

            # load
            with open('YOUR_PATH_TO_DATA/Takeout/Location History/Records.json') as data_file:    
                data = json.load(data_file)
            df = pd.json_normalize(data, 'locations')
            
            # get only relevant variables
            df = df[['latitudeE7', 'longitudeE7', 'timestamp']]
            
            # tranform them to be useful
            df.timestamp = pd.to_datetime(df.timestamp)
            df = df.assign(
                lat=df['latitudeE7']/1e7,
                long=df['longitudeE7']/1e7,
                year=df['timestamp'].dt.year,
                month=df['timestamp'].dt.month,
                day=df['timestamp'].dt.day,
                dow=df['timestamp'].dt.day_name(),
                time=df['timestamp'].dt.time,
            )

            

As a quick validity check, let's use the geopandas package to visualize all our different coordinates. Google has data on my locations since 2012, so this plot should include most of my locations over the past decade (i.e. concentrated on the two US coasts).

            import geopandas as gpd
            from shapely.geometry import Point
            import matplotlib.pyplot as plt

            # set up data structure of coordinates
            geo = [Point(xy) for xy in zip(df.long, df.lat)]
            gdf = gpd.GeoDataFrame(df, geometry=geo)

            # plot
            world = gpd.read_file(gpd.datasets.get_path('naturalearth_lowres'))
            gdf.plot(ax=world.plot(figsize=(14,14), color='lightgrey'), color="#7397CB")
            

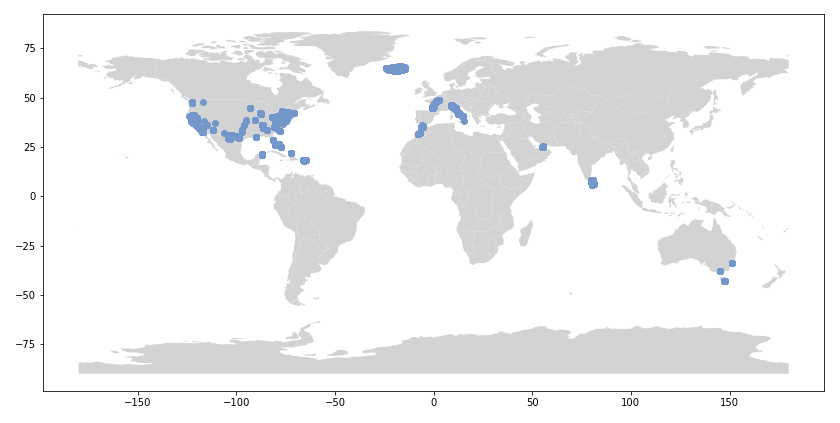Great! Now we're going filter down to the specific week where I was in Iceland

            st =  '2017-07-31'
            en = '2017-08-07'
            iceland = df[(df['timestamp'] >= st) & (df['timestamp'] <= en)]

            # remove duplicate lat/long pairs
            iceland = iceland.drop_duplicates(subset=['lat', 'long', 'day', 'month'])
            

Now that we have the data we'll be working with, we're ready to move on to working with road networks.

Visualizing your paths through road networks

We'll be using two Python packages to help visualize my path through Iceland: OSMnx, and networkX. OSMnx has data about road maps for most of the world. networkX allows us to use graph data structures to get information about the road networks. Both packages leverage some ideas and terminology from graph theory that we're going to go over before starting. A network or graph is a representation of system of two or more separable units (called nodes) and the interactions between them (called edges). Visually, nodes are often depicted as circles, with edges between them depicted as lines. In our case, edges are going to be roads and nodes are any intersections or decision points in those roads.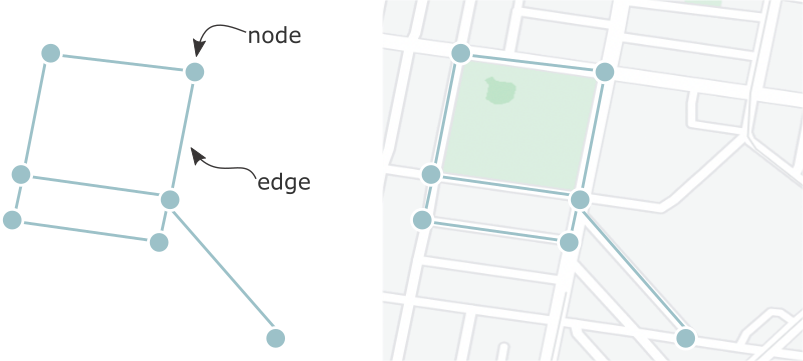 First, let's get a graph representation of Iceland's roads

            import osmnx as ox

            ox.config(log_console=True, use_cache=True)
            # location of graph
            place     = 'Iceland'
            # find shortest route based on the mode of travel (for our purposes it doesnt really matter which one)
            mode      = 'walk'        # 'drive', 'bike', 'walk'
            # find shortest path based on which feature
            optimizer = 'length'        # 'length','time'
            # create graph 
            graph = ox.graph_from_place(place, network_type = mode)
            

What exactly is this graph object we just made?

            type(graph)
            

Output:

            networkx.classes.multidigraph.MultiDiGraph
            

This is a networkX object. This means we can use functions and attributes from networkX to get properties of the graph. For example, we can get the density (or proportion of possible connections present) and number of edges in this graph.

            import networkx as nx

            print(nx.density(graph))
            print(len(graph.get_edges()))
            

Output:

            1.9575729910546824e-05
            

            327816
            

We're now going to use networkX to get paths between nodes that correspond to my location data. Our strategy for calculating my trajectory on this graph is as follows: get a starting coordinate; snap it to the closest spot on the road network; get an ending coordinate; snap it to the network; get the shorted path between the start and end coordinate; repeat. We can code up this strategy as follows:

            route = []
            start_latlng = (iceland['lat'].values[0],iceland['long'].values[0])
            
            # find the nearest node to the start location
            orig_node = ox.get_nearest_node(graph, start_latlng)
            
            # get the rest of the path
            for i in range(len(iceland) - 1):
                # define the end location in latlng
                end_latlng = (iceland['lat'].values[i+1],iceland['long'].values[i+1])
                # find the nearest node to the end location
                dest_node = ox.get_nearest_node(graph, end_latlng)
                #  find the shortest path
                route.extend(nx.shortest_path(graph,
                                        orig_node,
                                        dest_node,
                                        weight=optimizer))
                # advance to the next step
                orig_node = dest_node
            

And then plot it

            from itertools import groupby 

            # remove any duplicates from the route - these cause the plotting to break
            route = [i[0] for i in groupby(route)]
            fig, ax = ox.plot_graph_route(graph,
                                            route,
                                            node_size=0,
                                            edge_linewidth=0.3,
                                            edge_color='white',
                                            route_color="#EB8D43",
                                            route_linewidth=1.5,
                                            route_alpha=1.0,
                                            orig_dest_size=0)
            

And here we have a visualization of my vacation. It's also important to note some limitations in this visualization. This method requires snapping to a road network. This might get incorrect locations at times when I was not on a true road, like on hikes or boats. Additionally, the shortest path between two points might not be the path that I took. This can lead to wrong data especially in cases where I travelled far between Google's recordings. Given these caveats, we can still observe some things about my path. While I did travel through most parts of the country, the path I took is very directed. No one area has dense coverage, and the path mostly sticks to the coast. These observations make sense given what I wanted to get out of the trip. I wanted to see as much of the country as possible in the week I was there. I also had prebooked accomodations in different cities for every night, which didn't allow me to wander or dwell in any one area. How could this have looked different? What if I had showed up to Iceland and just wandered the streeets of Reykjavik, turning randomly whenever I felt like it? What if I turned mostly randomly, but had tried to avoid places I had been before?

Random walkers

All these strategies can be coded up by imagining some agent who stands on a given node, and iteratively 'walks' to other connected nodes based on some rules. The rules are called 'biases', and sometimes even simple biases can lead to agents with behaviors that closely mimic real-world behaviors. Even when they don't, they can identify how much of the variance in a behavior is explained by simple rules and help better identify which features we don't yet understand. We'll go over a few examples below We'll start off looking what an unbiased random walker would do one the streets of Iceland (starting in Reykjavik), for a few different path lengths

            # scaling factor for length of walk
            c = 1 # plots shown for 1, 2, and 10
            # intialize
            start_latlng = (iceland['lat'].values[i],iceland['long'].values[i])
            orig_node = ox.get_nearest_node(graph, start_latlng)
            random_route = [orig_node]

            # get the walk
            for k in range(n):
                # pick a node of the proper step size
                next_node = list(graph.neighbors(orig_node))
                # get random selection for next step
                dest_node = np.random.choice(next_node)
                
                # only add to our route
                random_route.append(dest_node)
                orig_node = dest_node
            

This algorithm looks a lot different from my path! It doesn't see the whole country, and in fact never really gets far out of Reyykjavik, even if it takes 10 times more steps than I do. This isn't surprising given how much more densely connected streets are inside of cities than outside of them. Once you're inside a city, more intersections will lead you into the city than out of it, leading to a spot where random walkers will tend to accumulate. Maybe if we try to to avoid intersections we've already seen, we can make sure that we get out of the city eventually.

We can add biases to this walk algorithm to make it less likely to revisit nodes that its already been too. This is accomplished by adding an additional parameter (\(r\)) that sets the relative probability of revisiting nodes already in the path versus visiting new ones.

            r = 0.01

            # get the walk
            for k in range(n):
                # get neighboring nodes
                next_node = list(graph.neighbors(orig_node))
                # get transition probabilities, weighted by revisits
                transition_prob = np.ones((len(next_node),))
                revisit_idx = [m in bias_random_route for m in next_node]
            
                # check if all nodes are revisits/new
                if (len(set(revisit_idx)) == 1):
                    # set equal probability
                    transition_prob = transition_prob*(1/len(transition_prob))
                else:
                    # parameter r determines bias
                    transition_prob[revisit_idx] = r*transition_prob[0]
                    # normalize so it sums to 1
                    transition_prob = transition_prob/sum(transition_prob)
                        
                # get random selection for next step
                dest_node = np.random.choice(next_node, size=1, replace=False, p=transition_prob)
                dest_node = dest_node[0] # unwrap from list
                
                # only add to our route
                bias_random_route.append(dest_node)
                orig_node = dest_node
            

This bias towards novelty does a little better. Now, we much more easily get out of the city, and even get to a different part of the island. But the areas it visits are still more densely explored than mine, and I still get more coverage of the island as whole.

There's a lot of ways we could build on this bias towards novelty to get more realistic looking walks. We could add a bias towards popular locations, force the walk to start and stop at the airport, or give the walker global knowledge of the graph and tell it to navigate efficiently to specific landmarks. But for now, we'll stop here, and appreciate the aesthetic differences in these few exploration styles.

Other resources

• This project was inspired by this twitter post by Dr. Iva Brunec
• In addition to the documentation, this post on OSMnx was useful
• Color scheme from the Channel Islands

Double/debiased machine learning

Light- to medium-math explanation of the method with tutorials, June, 2022

What is double machine learning

To me -- and potentially, its creator -- Double Machine Learning sounds like a trendy name you would give a method to try to sound impressive in developer spaces. Double (or debiased) machine learning is actually a way to estimate specific causal effects in large, complex data [1]. Previously many causal modeling methods relied on assuming a specific form of the data rather than learning it - namely assuming that variables were normally distributed and linearly related to each other. In addition to these faulty assumptions, these methods don't allow for complex data where the entropy of the parameter space increases with increasing observations (in other words - most large, modern datasets). Combined, these features made causal inference difficult to apply to realworld problems.

A method called double machine learning (DML) allows causal inference to coexist with complex data with few assumptions, which has drummed up a lot of well-deserved excitement about the method (primarily in economics). When I was trying to learn more about DML, I found that there weren't as many resources out there as I had hoped and that most of the resources that were out there took a very theoretical approach. I wanted to create a resource that explained the theory at a higher level and had a larger emphasis on code based explainations. This post focuses on understanding how the DML algorthim works. If you want to skip to the application, you can look at my my second DML post and this tutorial from econML.

What clinical problems can DML be used for?

The creation of this methods aligns nicely with some trends in clinical informatics (my current field). Clinical machine learning projects have made a major push towards building risk or diagnostic models. Less attention has been devoted to using machine learning to suggest treatments or interventions. DML presents one path forward - for a particular causal structure. We can illustrate that structure like this: Here, Y is some clinical outcome of interest (risk of disease, probability of diagnosis, etc.). T is some treatment or intervention. X is all the relevant demographic, medical and social features of the patients. This diagram is illustrating that the treatment will influence the risk of disease, and that features of the patient will influence both the risk and which/whether treatments will be given. When clinician are deciding which treatments to give, it would be helpful to know the size of the arrow connecting T and Y (referred to now as the treatment effect). Specifically, we'd want the estimation of the treatment effect to:

1. be accurate with a lot of data (might seem obvious, but this is harder than it sounds)
2. come with confidence intervals
3. not make strict assumptions about the form of the data (leverage machine learning)

A method that provides these kinds of treatment effect estimates could prove to be a powerful tool for clinical bioinformatics moving forward.

DML's solution

These points have historically been hard to acheive because methods for 'good' causal estimates typically do not give us point 3, and methods of machine learning typically do not give us point 1 (and sometimes 2). Machine learning models do not give good causal estimates for 2 reasons:

1. Regularization, necessary for fitting complex data, induces a bias (think bias variance trade-ff). To reduce overfitting, analysts using machine learning methods often use regularization. However, this necessarily increases the bias of estimates.
2. Despite our best efforts, machine learning models fit on data that follow the causal diagram above tend to overfit data, further biasing results.

DML can remove those two sources of bias and give us an estimate of the treatment effect and all the extra points outlined above. At a high level, these biases are alleviated by fitting two separate machine learning models (thus the name) to estimate the effect of X on Y and T, and then solving for theta using the residuals of those estimates (more details on this below). Additionally, there are now some pretty good packages implementing DML in python that play nicely with scikit learn. All together, making it a desireable new method for applied scientists, and motivating me to give it a try.

Caveats and alternatives

Like all methods, DML comes with important assumptions and caveats. Assumptions (most of these are true of many causal methods):

1. Consistency - An individual's potential outcome under their observed exposure history is precisely their observed outcome.
2. Positivity - Everyone in the study has some probability of receiving treatment
3. You are recording all variables that influence Y and T in X. I think this is the most fraught assumption in medical contexts [2].

If these assumptions are not met, then the resulting estimate canot be interpretted causally. That's not to say it isn't useful, but it changes the types of conclusions we can draw. With these assumptions fulfilled, we can accurately say that "the treatment effect was calculated to be X%". Without it, we can say that, "the proportion of observations who experienced the outcome, after adjusting for baseline confounders, was estimated to be X% higher for those who received treatment compared to those who did not."

Caveats:

1. categorical treatment - at the moment, there isn't a way to use DML for a categorical treatment variable that also provides confidence intervals. Other methods, such as doubly robust learning, might be better suited here.
2. biased data classes - DML is known to be biased in cases where one outcome is extremely rare (though it is less biased than many other methods). Over/undersampling of the data might be helpful in these cases.

Alternatives

1. Doubly robust learning
2. Targetted minimum loss based estimation (TLME)
3. Bayesian Additive Regression Trees (BART)
4. Bayesian Causal Forest (BCF)

How DML allows causal inference and machine learning to mix

We're now going to describe the method in more detail than the above summary. The goal here is to hit the major points of the DML paper [1] restructured for a more applied audience.

Direct method

To formalize the problems and solutions discussed above, we're going to have to be more mathematically precise with our definitions. We're going to start by defining a specific formula for generating data. $$ {Y = T\theta_{0} + g_{0}(X) + U, E[U | X,T] = 0]} $$ $$ {T = m_{0}(X) + V, E[V | X] = 0} $$ Let's walk through the terms:

• \(X\) the features
• \(Y\) the outcome
• \(T\) the treatment (it can be binary, continuous, or categorical)
• \(g_0(x)\) some mappong of x to y, excluding the effect of T and $\theta_0$
• \(m_0(x)\) some mapping of x to t
• \(\theta\) - the treatment effect. Here its a scalar, for simplicity, but this doesn't have to be the case
• \(U, V\) the noise, which cancels out on average

This equation is essentially formalizing the graph we had displayed earlier. These equations are a useful example because they give us a specific functional form for how \(T\) affects \(Y\) (\(T \times \theta_0\)). Since this relationship is linear, it makes some of the math a little bit nicer. In the end, we want DML to work for more than just this specific situation, but this definition is useful for now. If we were to code up these relationships in python, it would look something like this. Note that to code this up we must pick a specific \(g_0(X)\) and \(m_0(X)\). It could be whatever you want, but here we're using some exponential sums of the first few columns of X (I picked this because that's what the original paper does).

 
            from scipy.linalg import toeplitz
            # pick any value for theta_0
            theta = -0.4

            # define a function for generating data
            def get_data(n, n_x, theta):
            """
            partially linear data generating process
            
            Inputs:
            n       the number of observations to simulate
            n_x     the number of columns of X to simulate
            theta   a scalar value for theta
            """
                cov_mat = toeplitz([np.power(0.7, k) for k in range(n_x)])
                x = np.random.multivariate_normal(np.zeros(n_x), cov_mat, size=[n, ])
            
                u = np.random.standard_normal(size=[n, ])
                v = np.random.standard_normal(size=[n, ])
                m0 = x[:, 0] + np.divide(np.exp(x[:, 2]), 1 + np.exp(x[:, 2]))
                t = m0 + u
                g0 =  np.divide(np.exp(x[:, 0]), 1 + np.exp(x[:, 0])) + x[:, 2]
                y = theta * t + g0 + v
                
                return x, y, t        
            >

Let's imagine you're given some X, T, and Y data, as well as the data generating equations above. You're then asked to estimate what theta is. One first attempt might be to build one machine learning model of \(T\theta_{0} + g_{0}(X)\) and \(g_0(X)\), then regress out \(T\) to solve for \(\theta_0\).

This is a little tricky because \(g_0(X)\) is not the influence of \(X\) on \(Y\), its the influence of \(X\) on the part of \(Y\) that isn’t influenced by \(T \times \theta_0\). Therefore, we have to do this iteratively: get an initial guess for \(\theta_0\) in order to estimate \(g_0(X)\); then use that estimate of \(g_0(X)\) to solve for \(\theta_0\). In code, the direct method would look like this:

First, we'd simulate our data, and build our machine learning estimate of \(Y\) from \(T\theta_{0} + g_{0}(X)\) (we'll call this model \(l_0(X)\))

 
            from sklearn.ensemble import RandomForestRegressor
        
            # get data
            x, y, t = get_data(n, n_x, theta)
                
            # this will be our model for predicting Y from X
            ml_l = RandomForestRegressor()
            ml_l.fit(x,y)
            >

Note that you could use whatever machine model you want, it doesn't have to be a random forest. In this example, it should be anything that can estimate exponential functions (since that's the form we picked for our data generating function). Next, we can take an initial guess for \(\theta_0\), and then fit our estimate of \(g_0(X)\)

 
            # this will be our model for predicting Y - T*theta from X, or g0_hat
            ml_g = RandomForestRegressor()
                
            # initial guess for theta
            l_hat = ml_l.predict(x)
            psi_a = -np.multiply(t, t)
            psi_b = np.multiply(t, y - l_hat)
            theta_init = -np.mean(psi_b) / np.mean(psi_a)
                
            # get estimate for g0
            ml_g.fit(x, y - t*theta_init)
            g_hat = ml_g.predict(x)
            >

Lastly, we can regress the effect of \(T\) our from our prediction

 
            # compute residuals
            u_hat = y - g_hat
            psi_a = -np.multiply(t, t)
            psi_b = np.multiply(t, u_hat)
                
            # get estimate of theta and and SE
            theta_hat = -np.mean(psi_b) / np.mean(psi_a)
            psi = psi_a * theta_hat + psi_b
            err = theta_hat - theta
            J = np.mean(psi_a)
            sigma2_hat = 1 / len(y) * np.mean(np.power(psi, 2)) / np.power(J, 2)
            err = err/np.sqrt(sigma2_hat)
            >

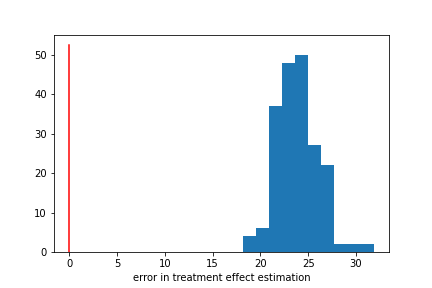If we repeat this process 200 times, we can genereate a histogram of our error term and see how well we did. If our estimate is good, we would expect the normalized difference between our estimate of \(\theta\) and the real theta to be centered on 0.

This histogram shows that is not the case. Our estimate is way off and centered on a positive value. What went wrong?

At a high level, part of what went wrong is that we did not explicitly model the effect of \(X\) on \(T\). That influence is biasing our estimate. Illustrating this explicitly is where our partially linear data generating process comes in handy. We can write out an equation for the error in our estimate. The goal here would be for the left-hand side to converge to 0 as we get more data.

regularization bias

\( \sqrt{n}(\hat{\theta_0} - \theta_0) = \) \((\frac{1}{n}\sum_{i\in I}^nT_{i}^2)^{-1}\frac{1}{\sqrt{n}}\sum_{i \in I}^nT_{i}U_{i}\) \(+\) \((\frac{1}{n}\sum_{i\in I}^nT_{i}^2)^{-1}\frac{1}{\sqrt{n}}\sum_{i \in I}^nT_{i}(g_0(X_i) - \hat{g_0}(X_i))\)

• The left hand side is our scaled error term - what we want to go to 0
• Noise cancels out on average, so this term is a very small number, divided by a big number. Essentially 0
• This term is where the problem is. Our estimate error is never going to be 0. This because of the deal we make as data scientists working with complex data. Reduce the varaince (overfitting) of our machine learning model, we induce some bias in our estimate (often through regularization). Additionally, \(T\) depends on \(X\), and therefore also will not converge to 0. Because of this, \(g_0-\hat{g} \times T\) will be small, but not 0. It will be divided by a large number, and will converge to 0 eventually, but too slowly to be practical.

We have to remove the effect of \(X\) on \(T\) to circumvent this bias. We can do this in three steps:

1. Estimate \(T\) from \(X\) using ML model of choice (different from the direct method!)
2. Estimate \(Y\) from \(X\) using ML model of choice
3. Regress the residuals of each model onto eachother to get \(\theta_0\)

We can write out a new error equation like so:

\(\sqrt{n}(\hat{\theta_0} - \theta_0) =\)\((EV^2)^{-1}\frac{1}{\sqrt{n}}\sum_{i \in I}^nU_iV_i\) \(+\) \((EV^2)^{-1}\frac{1}{\sqrt{n}}\sum_{i \in I}^n(\hat{m_0}(X_i) - m_0(X_i))(\hat{g_0}(X_i) - g_0(X_i))\) \(+ ... \)

• The left hand side is the same as before
• Noise cancels out on average, so this term is a very small number, divided by a big number. Essentially 0
• Now we have two small, non-0 numbers multiplied by eachother, divided by a large number. This will converge to 0 much more quickly than before
• ... this method adds a new term that we're going to ignore for now. But it comes back later!

In code, this new process only differs in the estimation \(g_0(X)\) amd \(\theta_0\). So fitting \(l_0(X)\) will be the same, but then we have:

 
            # model for predicting T from X - new to the regularized version!
            ml_m = RandomForestRegressor()
            # model for predicting Y - T|X*theta from X
            ml_g = RandomForestRegressor()
            
            ml_m.fit(x,t)
            m_hat = ml_m.predict(x)

            # this is the part that's different
            v_hat = t - m_hat
            psi_a = -np.multiply(v_hat, v_hat)
            psi_b = np.multiply(v_hat, y - l_hat)
            theta_init = -np.mean(psi_b) / np.mean(psi_a)
                
            # get estimate for G
            ml_g.fit(x, y - t*theta_init)
            g_hat = ml_g.predict(x)
            >

Similarly, when we get our final estmimate for \(\theta\)

    
            # compute residuals
            u_hat = y - g_hat
            # v_hat is the residuals from our m0 model
            psi_a = -np.multiply(v_hat, v_hat)
            psi_b = np.multiply(v_hat, u_hat)
                
            theta_hat = -np.mean(psi_b) / np.mean(psi_a)
            psi = psi_a * theta_hat + psi_b
            err = theta_hat - theta
            J = np.mean(psi_a)
            sigma2_hat = 1 / len(y) * np.mean(np.power(psi, 2)) / np.power(J, 2)
            err = err/np.sqrt(sigma2_hat)
            >

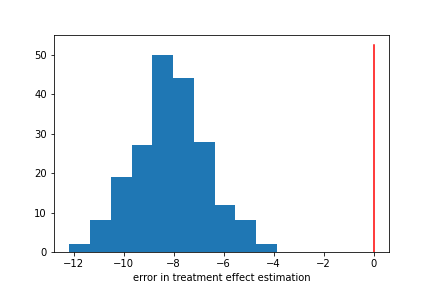If we plot a similar histogram over 200 simulations, we'll get something like this: And we have greatly reduced (but not eliminated) our bias!

For this specific data generating process, we now have a way of estimating \(\theta\) without regularization bias! However, I mentioned earlier that we want to be able to estimate more than only this process. In particular, step three involves linear regression, and only works in our partially linear example. How do we generalize the method of estimating \(\theta\)?

The least squares solution for linear relationships essentially finds the parameters for a line that minimizes the error between the predicted points on the line, and the observed data. We can write this as the minimization of a cost function of our data and true parameters $$ \psi(W; \theta, \eta) = 0 $$ This equation looks vary different but contains a lot of the same players as before:

1. \(W\) is the data (\(X\),\(Y\), and \(T\))
2. \(\theta\) is the true treatment effect
3. \(\psi\) is just some cost function. We are purposely not defining it because we want this to be a general solution, but you can think of it as any kind of error minimization function
4. \(\eta\) is called the nuisance parameter, and here contains \(g\) and \(m\)

Solving minimization problems like these are often difficult and subject to noise. To assure we find a robust solution, we're going to add one other condition to our equation (called a moment condition) $$ { \delta_{\eta}E[\psi(W; \theta, \eta][\eta - \eta_0] = 0} $$ Technically, this is a direction al Gateaux derivative. Practically, what this means is that we expect that the true value of \(\theta\) would be robust to small purturbations in the nuisance parameters. This has the benefit of giving use estimates that will be stable in the presence of small changes to our ML models.

There are whole branches of mathematics dedicated to solving these types of equations with moment conditions, and there is no single good solution. All the different solutions are called 'DML estimators'. Rather than getting into any specific estimator here, we're just going to trust that they exist, and move on. Whatever package you use to apply the method should give some information on the estimators it implements.

We now have a more generalizable set of steps

1. Estimate \(T\) from \(X\)
2. Estimate \(Y\) from \(X\)
3. Solve moment equation to get \(\theta\)

overfitting bias

We now have a generalizable solution to regularization bias. Additionally, with the definition of a cost function, we have a method of evaluating our DML estimator and comparing different models. Specifically, we can find the model that gives smallest value for our moment condition. The specific value of this function is usually called a 'score' or 'Neyman orthogonality score', and the closer to 0 it is the better. We would use this value to perform model selection when applying this method.

Now, it's time to revisit out error equation in the partially linear case. $$ { \sqrt{n}(\hat{\theta_0} - \theta_0) = (EV^2)^{-1}\frac{1}{\sqrt{n}}\sum_{i \in I}^nU_iV_i + (EV^2)^{-1}\frac{1}{\sqrt{n}}\sum_{i \in I}^n(\hat{m_0}(X_i) - m_0(X_i))(\hat{g_0}(X_i) - g_0(X_i)) + \frac{1}{\sqrt{n}}\sum_{i \in I}^{n}V_i(\hat{g_0}(X_i) - g_0(X_i)) } $$ We've discussed the first two terms already, but I'm revealing the last term we had hidden previously. If any overfitting is present in \(\hat{g_0}\), the estimate will pick up some noise from the noise term \(U\). This will slow down the convergence of this new term to 0.

The solution to this bias is to fit \(g\) and \(m\) on a different set of data than the set used to estimate \(\theta\). Like how cross-validation avoids overfitting during parameter selection, this method (called cross-fitting) avoids overfitting in our estimation of \(\theta\). This changes our DML steps slightly.

1. Split the data into \(K\) folds. For each fold:
2. Estimate \(T\) from \(X\) using ML model of choice and fold \(K\)
3. Estimate \(Y\) from \(X\) using ML model of choice and fold \(K\)
4. Solve moment equation get \(\theta\) using other sets of data
5. Select \(\theta\) estimate that gives the best solution over all splits.

In code, all this does is add a loop over folds:

            from sklearn.model_selection import KFold
            # number of splits for cross fitting
            nSplit = 2
            x, y, t = get_data(n, n_x, theta)

            # cross fit
            kf = KFold(n_splits=nSplit)
            # save theta hats, and some variables for getting variance in theta_hat
            theta_hats = []
            sigmas = []
                for train_index, test_index in kf.split(x):
                    x_train, x_test = x[train_index], x[test_index]
                    y_train, y_test = y[train_index], y[test_index]
                    t_train, t_test = t[train_index], t[test_index]

                    ml_l = RandomForestRegressor()
                    ml_m = RandomForestRegressor()
                    ml_g = RandomForestRegressor()

                    ml_l.fit(x_train,y_train)
                    ml_m.fit(x_train,t_train)
                    l_hat = ml_l.predict(x_test)
                    m_hat = ml_m.predict(x_test)

                    # initial guess for theta
                    u_hat = y_test - l_hat
                    v_hat = t_test - m_hat
                    psi_a = -np.multiply(v_hat, v_hat)
                    psi_b = np.multiply(v_hat, u_hat)
                    theta_init = -np.mean(psi_b) / np.mean(psi_a)

                    # get estimate for G
                    ml_g.fit(x_train, y_train - t_train*theta_init)
                    g_hat = ml_g.predict(x_test)

                    # compute residuals
                    u_hat = y_test - g_hat

                    psi_a = -np.multiply(v_hat, v_hat)
                    psi_b = np.multiply(v_hat, u_hat)

                    theta_hat = -np.mean(psi_b) / np.mean(psi_a)
                    theta_hats.append(theta_hat)
                    psi = psi_a * theta_hat + psi_b
                    sigma2_hat = 1 / len(y_test) * np.mean(np.power(psi, 2)) / np.power(J, 2)
                    sigmas.append(sigma2_hat)
                err = np.mean(theta_hat) - theta
                err = err/np.sqrt(np.mean(sigmas))
            

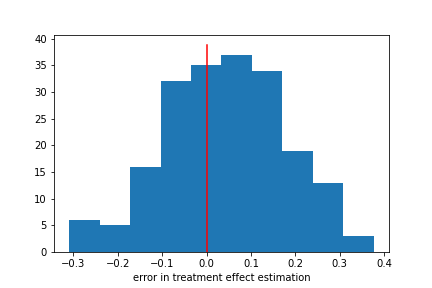Using this process, we can correct the bias in our estimation Now we have a pretty good estimate! So far, we've gone over what the DML method is, and how is overcomes biases from regularization and overfitting to get good estimates of \(\theta\) without making strong assumptions about the form of the data. There are two packages (econML and DoubleML) that allow for applications of this method in Python and R. I have an application post that walks through an example using econML. Hopefully this post made the method little more accessible or helped you assess if this method would be a good fit for your data.

Other resources

• This blog post on DML
• I liked these slides so much I risked the social humiliation that comes with liking a twitter post from years ago to show my support
• DoubleML github (see this for code to exactly replicate the figures in the paper)

References

1. Chernozhukov, V., Chetverikov, D., Demirer, M., Duflo, E., Hansen, C., Newey, W., & Robins, J. (2016). Double/Debiased Machine Learning for Treatment and Causal Parameters. http://arxiv.org/abs/1608.00060
2. Rose, S., & Rizopoulos, D. (2020). Machine learning for causal inference in Biostatistics. In Biostatistics (Oxford, England) (Vol. 21, Issue 2, pp. 336–338). NLM (Medline). https://doi.org/10.1093/biostatistics/kxz045